Difference between revisions of "De Vahl Davis natural convection test"
(→Code) |
(→Code) |
||
| Line 26: | Line 26: | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| − | // | + | v2[boundary] = vec_t{0.0, 0.0}; |
| − | + | T2[left] = O.T_cold; | |
| − | + | T2[right] = O.T_hot; | |
| − | + | //Time stepping | |
| − | + | for (int step = 0; step <= O.t_steps; ++step) { | |
| − | + | for (int i_count = 1; i_count < _MAX_ITER_; ++i_count) { | |
| − | + | // Navier Stokes | |
| − | + | for (auto c : interior) { | |
| − | + | v2[c] = v1[c] + O.dt * (-1 / O.rho * op.grad(P1, c) | |
| − | + | + O.mu / O.rho * op.lap(v1, c) | |
| − | + | - op.grad(v1, c) * v1[c] | |
| − | + | + O.g * (1 - O.beta * (T1[c] - O.T_ref))); | |
| − | + | } | |
| − | } | + | |
| − | + | //Speed of sound | |
| − | + | Range<scal_t> norm = v2.map([](const vec_t& p) { return p.norm(); }); | |
| − | + | scal_t C = O.dl * std::max(*std::max_element(norm.begin(), norm.end()), O.v_ref); | |
| − | + | // Mass continuity | |
| − | + | Range<scal_t> div_v; | |
| − | + | for (auto c:all) { | |
| − | + | div_v[c] = op.div(v2, c); | |
| − | + | P2[c] = P1[c] - C * C * O.dt * O.rho * div_v[c] + | |
| − | + | O.dl2 * C * C * O.dt * O.dt * op.lap(P1, c); | |
| − | + | } | |
| − | + | P1.swap(P2); | |
| − | + | } | |
| − | + | ||
| − | + | //heat transport | |
| − | + | for (auto c : interior) { | |
| − | + | T2[c] = T1[c] + O.dt * O.lam / O.rho / O.c_p * op.lap(T1, c) - | |
| − | } | + | O.dt * v1[c].transpose() * op.grad(T1, c); |
| − | + | } | |
| − | + | for (auto c : top) T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0); | |
| − | + | for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0); | |
| − | + | } | |
</syntaxhighlight> | </syntaxhighlight> | ||
=Results= | =Results= | ||
Revision as of 13:15, 29 November 2017
Intro
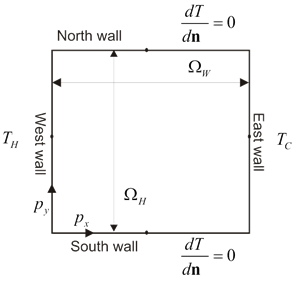
The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^5}$. Here we present a MLSM solution of the case.
\begin{equation} \text{Ra}\text{=}\,\frac{\left| \mathbf{g} \right|{{\beta }_{T}}\left( {{T}_{H}}-{{T}_{C}} \right){{\Omega }_{H}}^{3}{{\rho }^{2}}{{c}_{p}}}{\lambda \mu } \end{equation} \begin{equation} \text{Pr}=\frac{\mu {{c}_{p}}}{\lambda } \end{equation}
[1] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64.
[2] Lage JL, Bejan A. The Ra-Pr domain of laminar natural convection in an enclosure heated from the side. Numer Heat Transfer. 1991;A19:21-41.
[3] Janssen RJA, Henkes RAWM. Accuracy of finite-volume disretizations for the bifurcating natural-convection flow in a square cavity. Numer Heat Transfer. 1993;B24:191-207.
[4] Nobile E. Simulation of time-dependent flow in cavities with the additive-correction multigrid method, part II: Apllications. Numer Heat Transfer. 1996;B30:341-50.
Code
The snippet of the openMP parallel MLSM code for an explicit ACM method with CBS looks like: (full examples, including implicit versions, can be found under the examples in the code repository Main Page).
1 v2[boundary] = vec_t{0.0, 0.0};
2 T2[left] = O.T_cold;
3 T2[right] = O.T_hot;
4 //Time stepping
5 for (int step = 0; step <= O.t_steps; ++step) {
6 for (int i_count = 1; i_count < _MAX_ITER_; ++i_count) {
7 // Navier Stokes
8 for (auto c : interior) {
9 v2[c] = v1[c] + O.dt * (-1 / O.rho * op.grad(P1, c)
10 + O.mu / O.rho * op.lap(v1, c)
11 - op.grad(v1, c) * v1[c]
12 + O.g * (1 - O.beta * (T1[c] - O.T_ref)));
13 }
14
15 //Speed of sound
16 Range<scal_t> norm = v2.map([](const vec_t& p) { return p.norm(); });
17 scal_t C = O.dl * std::max(*std::max_element(norm.begin(), norm.end()), O.v_ref);
18 // Mass continuity
19 Range<scal_t> div_v;
20 for (auto c:all) {
21 div_v[c] = op.div(v2, c);
22 P2[c] = P1[c] - C * C * O.dt * O.rho * div_v[c] +
23 O.dl2 * C * C * O.dt * O.dt * op.lap(P1, c);
24 }
25 P1.swap(P2);
26 }
27
28 //heat transport
29 for (auto c : interior) {
30 T2[c] = T1[c] + O.dt * O.lam / O.rho / O.c_p * op.lap(T1, c) -
31 O.dt * v1[c].transpose() * op.grad(T1, c);
32 }
33 for (auto c : top) T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0);
34 for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0);
35 }