Difference between revisions of "De Vahl Davis natural convection test"
| Line 1: | Line 1: | ||
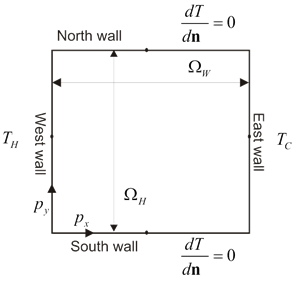
The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^[5]}$. Here we present a MLSM solution of the case. | The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^[5]}$. Here we present a MLSM solution of the case. | ||
| + | |||
| + | $\text{R}{{\text{a}}_{T}}\text{=}\,\frac{\left| \mathbf{g} \right|{{\beta }_{T}}\left( {{T}_{H}}-{{T}_{C}} \right){{\Omega }_{H}}^{3}{{\rho }^{2}}{{c}_{p}}}{\lambda \mu }$, | ||
| + | |||
| + | \[\text{Pr}=\frac{\mu {{c}_{p}}}{\lambda }\], | ||
[1] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64. | [1] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64. | ||
Revision as of 15:26, 22 October 2017
The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^[5]}$. Here we present a MLSM solution of the case.
$\text{R}{{\text{a}}_{T}}\text{=}\,\frac{\left| \mathbf{g} \right|{{\beta }_{T}}\left( {{T}_{H}}-{{T}_{C}} \right){{\Omega }_{H}}^{3}{{\rho }^{2}}{{c}_{p}}}{\lambda \mu }$,
\[\text{Pr}=\frac{\mu {{c}_{p}}}{\lambda }\],
[1] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64.
[2] Lage JL, Bejan A. The Ra-Pr domain of laminar natural convection in an enclosure heated from the side. Numer Heat Transfer. 1991;A19:21-41.
[3] Janssen RJA, Henkes RAWM. Accuracy of finite-volume disretizations for the bifurcating natural-convection flow in a square cavity. Numer Heat Transfer. 1993;B24:191-207.
[4] Nobile E. Simulation of time-dependent flow in cavities with the additive-correction multigrid method, part II: Apllications. Numer Heat Transfer. 1996;B30:341-50.
The snippet of the openMP parallel MLSM code for an explicit ACM method with CBS looks like: (full examples, including implicit versions, can be found under the examples in the code repository Main Page).
1 //transport equations
2 //transport equations
3 #pragma omp parallel for private(i) schedule(static)
4 for (i=0;i<interior.size();++i) {
5 int c=interior[i];
6 //Navier-Stokes
7 v2[c] = v1[c] + O.dt * ( - 1/O.rho * op.grad(P1,c)
8 + O.mu/O.rho * op.lap(v1, c)
9 - op.grad(v1,c)*v1[c]
10 + O.g*(1 - O.beta*(T1[c] - O.T_ref))
11 );
12 //heat transport
13 T2[c] = T1[c] + O.lam / O.rho / O.c_p * O.dt * op.lap(T1, c)
14 -O.dt*O.rho*O.c_p * v1[c].transpose()*op.grad(T1,c) ;
15 }
16 //heat Neumann condition
17 #pragma omp parallel for private(i) schedule(static)
18 for (i=0;i<top.size();++i) {
19 int c = top[i];
20 T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0);
21 }
22
23 #pragma omp parallel for private(i) schedule(static)
24 for (i=0;i<bottom.size();++i) {
25 int c = bottom[i];
26 T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0);
27 }
28
29 //Mass continuity
30 #pragma omp parallel for private(c) schedule(static)
31 for (i=0; i<domain.size(); ++i) {
32
33 P2[i] = P1[i] - O.dl * O.dt * O.rho * op.div(v2, i) +
34 O.dl2 * O.dl * O.dt * O.dt * op.lap(P1, i);
35 }
36 //time step
37 v1.swap(v2);
38 P1.swap(P2);
39 T1.swap(T2);