Revision as of 07:19, 3 October 2017 (view source) Jureslak (talk | contribs) ← Older edit		Revision as of 07:20, 3 October 2017 (view source) Jureslak (talk | contribs) Newer edit →
Line 5:		Line 5:
	9(8) (2016), doi:10.3390/ma9080639. </ref> and described in detail in Hojjati-Talemi et al. (2014) <ref>R. Hojjati-Talemi, M. A. Wahab in dr., Prediction of fretting fatigue crack		9(8) (2016), doi:10.3390/ma9080639. </ref> and described in detail in Hojjati-Talemi et al. (2014) <ref>R. Hojjati-Talemi, M. A. Wahab in dr., Prediction of fretting fatigue crack
	initiation and propagation lifetime for cylindrical contact configuration, Tribol. Int. 76 (2014) 73–91, doi:10.1016/j.triboint.2014.02.017. </ref>		initiation and propagation lifetime for cylindrical contact configuration, Tribol. Int. 76 (2014) 73–91, doi:10.1016/j.triboint.2014.02.017. </ref>
		+
		+	== Description of the case and parameters ==
		+
		+	= MLSM numerical solution for bulk load =
		+	== Case definition ==
		+
		+	We are solving the equation $$(\lambda + \mu) \nabla (\nabla \cdot \b{u}) + \mu \nabla^2 \b{u} = 0$$
		+	on the domain $D = [-L/2, L/2] \times [-H/2, 0]$. Componentwise $\b{u} = [u; v]$.
		+	The boundary conditions are:
		+	* top: $\vec{t}(x) = (q(x), -p(x))$ or componentwise $\mu \frac{\partial u}{\partial y}(x, 0) + \mu \frac{\partial v}{\partial x}(x, 0) = q(x)$ and $(2 \mu+\lambda) \frac{\partial u}{\partial x}(x, 0) + \lambda \frac{\partial v}{\partial y}(x, 0) = -p(x)$ .
		+	* left: $\b{u} = 0$ or componentwise $u(-L/2, y) = v(-L/2, y) = 0$.
		+	* bottom: up-down symmetry conditions: componentwise $\frac{\partial u}{\partial y}(x, -H/2) = 0, v(x, -H/2) = 0$.
		+	* right: this part is traction free, ie. $\vec{t}(y) = 0$ or componentwise $\mu \frac{\partial u}{\partial y}(L/2, y) + \mu \frac{\partial v}{\partial x}(L/2, y) = 0$ and $(2 \mu+\lambda) \frac{\partial v}{\partial y}(L/2, y) + \lambda \frac{\partial u}{\partial x}(L/2, y) = 0$.
		+
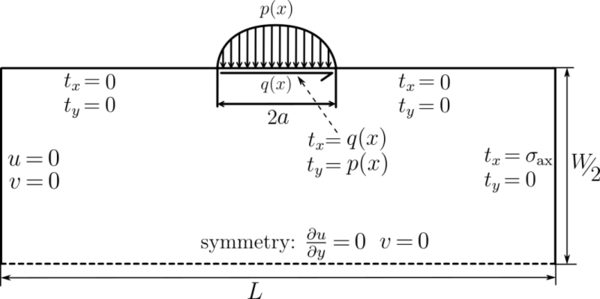
		+	Illustration of the computational domain is presented below.
		+
		+	[[File:fwo_bc.png|600px]]
		+
		+	== Phsyical parameters ==
		+	Basic parameters are:
		+	* $E = \unit{72.1}{GPa}$, Youngs modulus
		+	* $\nu = 0.33$, Poissons ratio
		+	* $L = \unit{40}{mm}$, length, width of the pad
		+	* $H = \unit{4}{mm}$, height, thickness of the pad
		+	* $\sigma_{ax} = \unit{100}{MPa}$, axial pressure
		+	* $F = \unit{543}{N}$, normal force
		+	* $Q = \unit{155}{N}$, tangential force
		+	* $R = \unit{10}{mm}$ or $\unit{50}{mm}$, raduis of curvature of the cylindrical pad
		+	* $COF = \mu = 0.3$ or $0.85$ or $2$, coefficient of friction
		+
		+	Derived parameters are, for choice of $R = \unit{10}{mm}$ and $\mu = 0.3$:
		+	* $E^\ast = \frac{E}{2(1-\nu^2)} = \unit{40.4}{GPa}$, combined Young's modulus
		+	* $p_{max} = p_0 = \sqrt{\frac{FE^\ast}{HR \pi}} = \unit{418.10407}{MPa}$, maximal normal pressure
		+	* $a = 2 \sqrt{\frac{FR}{HE^\ast \pi}} = \unit{0.2067}{mm}$, semi contact width, contact region is $[-a, a] \times \{0\}$
		+	* $c = a \sqrt{1 - \frac{Q}{\mu F}} = \unit{0.04504}{mm}$, stick zone semi width
		+	* $e = \frac{a \sigma_{ax}}{4 \mu p_{max}} = \unit{0.041197}{mm}$, eccentricity due to axial load
		+
		+	== Numerical solution ==
		+
		+	Comparison of this solution against FEM solution published in Pereira et al. (2016) is presented below.
		+
		+	[[File:fwo_cases.png|800px]]
		+
		+	The data for this plot (only MLSM data) is available to download here: [[:File:fwo_cases_data.csv]].
		+
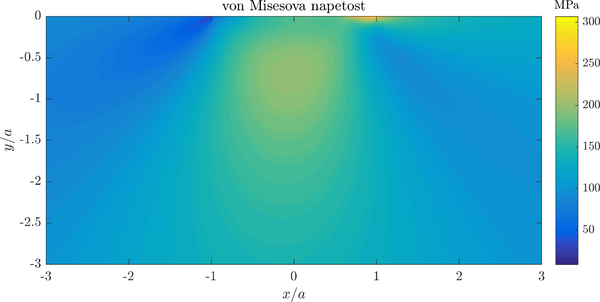
		+	A contour plot of von Mises stress in the specimen is presented below.
		+
		+	[[File:fwo_solution.png|600px]]
		+
		+	Note that contour of stress are similar to the ones in Hertzian contact above, but a significant concentracion of stresses under the contact area is present.

---

Revision as of 07:20, 3 October 2017

Click on Solid Mechanics to go back.

Introdution

This case is an extension of the classical Hertzian contact, as defined in Pereira et al. (2016) ^[1] and described in detail in Hojjati-Talemi et al. (2014) ^[2]

Description of the case and parameters

MLSM numerical solution for bulk load

Case definition

We are solving the equation $$(\lambda + \mu) \nabla (\nabla \cdot \b{u}) + \mu \nabla^2 \b{u} = 0$$ on the domain $D = [-L/2, L/2] \times [-H/2, 0]$. Componentwise $\b{u} = [u; v]$. The boundary conditions are:

• top: $\vec{t}(x) = (q(x), -p(x))$ or componentwise $\mu \frac{\partial u}{\partial y}(x, 0) + \mu \frac{\partial v}{\partial x}(x, 0) = q(x)$ and $(2 \mu+\lambda) \frac{\partial u}{\partial x}(x, 0) + \lambda \frac{\partial v}{\partial y}(x, 0) = -p(x)$ .
• left: $\b{u} = 0$ or componentwise $u(-L/2, y) = v(-L/2, y) = 0$.
• bottom: up-down symmetry conditions: componentwise $\frac{\partial u}{\partial y}(x, -H/2) = 0, v(x, -H/2) = 0$.
• right: this part is traction free, ie. $\vec{t}(y) = 0$ or componentwise $\mu \frac{\partial u}{\partial y}(L/2, y) + \mu \frac{\partial v}{\partial x}(L/2, y) = 0$ and $(2 \mu+\lambda) \frac{\partial v}{\partial y}(L/2, y) + \lambda \frac{\partial u}{\partial x}(L/2, y) = 0$.

Illustration of the computational domain is presented below.

Phsyical parameters

Basic parameters are:

• $E = \unit{72.1}{GPa}$, Youngs modulus
• $\nu = 0.33$, Poissons ratio
• $L = \unit{40}{mm}$, length, width of the pad
• $H = \unit{4}{mm}$, height, thickness of the pad
• $\sigma_{ax} = \unit{100}{MPa}$, axial pressure
• $F = \unit{543}{N}$, normal force
• $Q = \unit{155}{N}$, tangential force
• $R = \unit{10}{mm}$ or $\unit{50}{mm}$, raduis of curvature of the cylindrical pad
• $COF = \mu = 0.3$ or $0.85$ or $2$, coefficient of friction

Derived parameters are, for choice of $R = \unit{10}{mm}$ and $\mu = 0.3$:

• $E^\ast = \frac{E}{2(1-\nu^2)} = \unit{40.4}{GPa}$, combined Young's modulus
• $p_{max} = p_0 = \sqrt{\frac{FE^\ast}{HR \pi}} = \unit{418.10407}{MPa}$, maximal normal pressure
• $a = 2 \sqrt{\frac{FR}{HE^\ast \pi}} = \unit{0.2067}{mm}$, semi contact width, contact region is $[-a, a] \times \{0\}$
• $c = a \sqrt{1 - \frac{Q}{\mu F}} = \unit{0.04504}{mm}$, stick zone semi width
• $e = \frac{a \sigma_{ax}}{4 \mu p_{max}} = \unit{0.041197}{mm}$, eccentricity due to axial load

Numerical solution

Comparison of this solution against FEM solution published in Pereira et al. (2016) is presented below.

800px

The data for this plot (only MLSM data) is available to download here: File:fwo_cases_data.csv.

A contour plot of von Mises stress in the specimen is presented below.

Note that contour of stress are similar to the ones in Hertzian contact above, but a significant concentracion of stresses under the contact area is present.

1. ↑ K. Pereira et al., On the convergence of stresses in fretting fatigue, Materials 9(8) (2016), doi:10.3390/ma9080639.
2. ↑ R. Hojjati-Talemi, M. A. Wahab in dr., Prediction of fretting fatigue crack initiation and propagation lifetime for cylindrical contact configuration, Tribol. Int. 76 (2014) 73–91, doi:10.1016/j.triboint.2014.02.017.