Difference between revisions of "Analysis of MLSM performance"
(→Solving Electrostatics) |
(→Solving Dirichlet with MLSM operators) |
||
| (48 intermediate revisions by 5 users not shown) | |||
| Line 21: | Line 21: | ||
<figure id="fig:square_heat"> | <figure id="fig:square_heat"> | ||
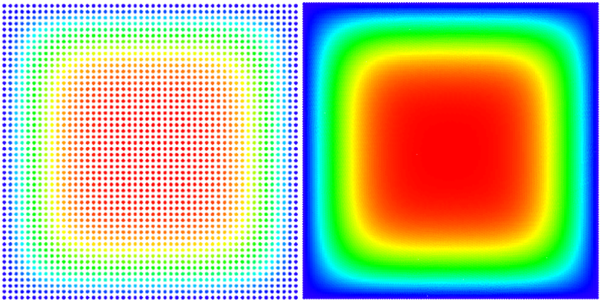
| − | [[File:square_heat.png|thumb|upright=2|alt=A square of nodes coloured according to the solution(with smaller and larger node density)|<caption>A picture of our solution (with smaller and larger node density)</caption>]] | + | [[File:square_heat.png|thumb|upright=2|center|alt=A square of nodes coloured according to the solution(with smaller and larger node density)|<caption>A picture of our solution (with smaller and larger node density)</caption>]] |
</figure> | </figure> | ||
| − | + | ==Convergence with respect to number of nodes== | |
| − | |||
| − | |||
<figure id="fig:node_convergence"> | <figure id="fig:node_convergence"> | ||
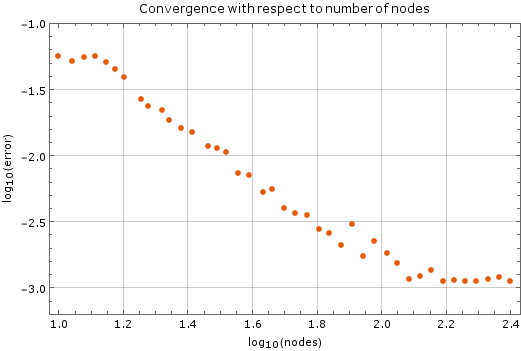
| − | [[File:node_convergence.png|thumb|upright=2|alt=Graph of errors with respect to number of nodes|<caption>Convergence with respect to number of nodes</caption>]] | + | [[File:node_convergence.png|thumb|upright=2|center|alt=Graph of errors with respect to number of nodes|<caption>Convergence with respect to number of nodes</caption>]] |
</figure> | </figure> | ||
| Line 43: | Line 41: | ||
<figure id="fig:node_convergence_5"> | <figure id="fig:node_convergence_5"> | ||
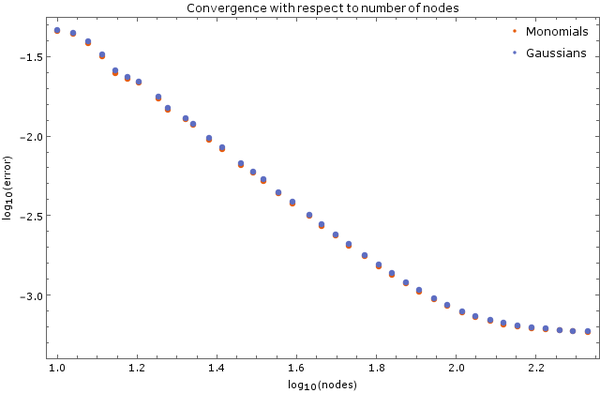
| − | [[File:node_convergence_5.png|thumb|upright=2|<caption>Convergence with respect to number of nodes for Gaussian and Monomial basis</caption>]] | + | [[File:node_convergence_5.png|thumb|upright=2|center|<caption>Convergence with respect to number of nodes for Gaussian and Monomial basis</caption>]] |
</figure> | </figure> | ||
| Line 51: | Line 49: | ||
Error was calculated after $0.01$ time units have elapsed. | Error was calculated after $0.01$ time units have elapsed. | ||
| − | ===Convergence with respect to number of time steps | + | <figure id="fig:node_convergence_comparison"> |
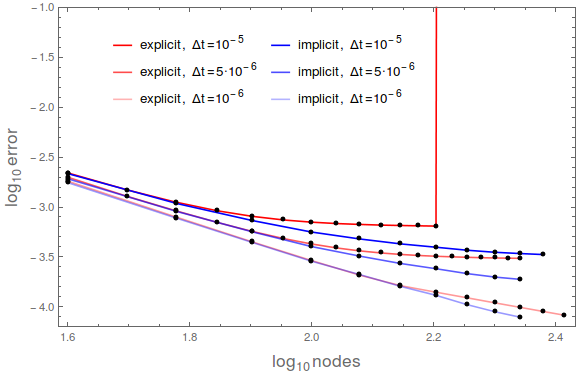
| + | [[File:explicit_implicit_diffusion_comparison_ver2.png|thumb|upright=2|center|<caption>Convergence with respect to number of nodes for explicit and implicit mixed boundary condition (Neumann is enforced in two different ways).</caption>]] | ||
| + | </figure> | ||
| + | |||
| + | Figure 4 shows convergence of 1/4 of the whole solution with Dirichlet boundary conditions (Fig. 1). The nodes were spanning the area $[0, a/2]^2$. As expected, higher number of nodes yields lower max error up to some maximal number of nodes. The latter is lower for explicit than for implicit method. | ||
| + | |||
| + | ==Convergence with respect to number of time steps== | ||
<figure id="fig:timestep_convergence"> | <figure id="fig:timestep_convergence"> | ||
| − | [[File:timestep_convergence.png|thumb|upright=2|<caption>Convergence with respect to different timesteps</caption>]] | + | [[File:timestep_convergence.png|thumb|upright=2|center|<caption>Convergence with respect to different timesteps</caption>]] |
</figure> | </figure> | ||
| Line 65: | Line 69: | ||
size was $n = 12$. | size was $n = 12$. | ||
| − | + | ==Using Gaussian basis== | |
<figure id="fig:gauss_sigma_dependence"> | <figure id="fig:gauss_sigma_dependence"> | ||
| − | [[File:gauss_sigma_dependence.png|thumb|upright=2|<caption> Graph of error with respect to Gaussian basis $\sigma$ </caption>]] | + | [[File:gauss_sigma_dependence.png|thumb|upright=2|center|<caption> Graph of error with respect to Gaussian basis $\sigma$ </caption>]] |
</figure> | </figure> | ||
| Line 82: | Line 86: | ||
appropriately, with respect to plot above. | appropriately, with respect to plot above. | ||
| − | ===Solving in 3D | + | == Convergence with respect to shape parameters == |
| + | |||
| + | Choice of shape of the basis function can have significant effect on solution of the system. | ||
| + | We tested the space of feasible shape parameters on the diffusion equation with $\Delta x = \Delta y = 0.01$ | ||
| + | and $m = n = 9$. The weight function does not have much influence here, except on the condition | ||
| + | number and any singular values that get cut off because of that. | ||
| + | |||
| + | Results for Gaussian, MQ and IMQ basis functions are presented in <xr id="fig:shape_space_gau"/>, <xr id="fig:shape_space_mq"/> and <xr id="fig:shape_space_imq"/>. | ||
| + | |||
| + | <figure id="fig:shape_space_gau"> | ||
| + | [[File:sigma_depedance_error_gau.png|thumb|left|800px|<caption>Error as a function of Gaussian basis' $\sigma_B$ and Gaussian weight's $\sigma_W$</caption>]] | ||
| + | </figure> | ||
| + | <figure id="fig:shape_space_mq"> | ||
| + | [[File:sigma_depedance_error_imq.png|thumb|800px|<caption>Error as a function of MQ basis' $\sigma_B$ and Gaussian weight's $\sigma_W$</caption>]] | ||
| + | </figure> | ||
| + | <figure id="fig:shape_space_imq"> | ||
| + | [[File:sigma_depedance_error_mq.png|thumb|upright=1|left|800px|<caption>Error as a function of IMQ basis' $\sigma_B$ and Gaussian weight's $\sigma_W$</caption>]] | ||
| + | </figure> | ||
| + | <figure id="fig:shape_space_imq"> | ||
| + | [[File:sigma_depedance_error_mon.png|thumb|upright=1|800px|<caption>Error as a function of Gaussian weight's $\sigma_W$ for Monomials of order 2.</caption>]] | ||
| + | </figure> | ||
| + | |||
| + | <div style="clear:both"></div> | ||
| + | |||
| + | ==Solving in 3D== | ||
A 3-dimensional case on domain $[0, 1]^3$ was tested on $N = 20^3$ | A 3-dimensional case on domain $[0, 1]^3$ was tested on $N = 20^3$ | ||
| Line 96: | Line 124: | ||
</figure> | </figure> | ||
| − | + | ==Solving mixed boundary conditions with MLSM operators== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
By using MLSM operators and utilizing its `[http://www-e6.ijs.si/ParallelAndDistributedSystems/MeshlessMachine/technical_docs/html/classmm_1_1MLSM.html MLSM::neumann]` method we can also solve | By using MLSM operators and utilizing its `[http://www-e6.ijs.si/ParallelAndDistributedSystems/MeshlessMachine/technical_docs/html/classmm_1_1MLSM.html MLSM::neumann]` method we can also solve | ||
partial diffusion equations. Solution is on <xr id="fig:quarter_diffusion"/>. | partial diffusion equations. Solution is on <xr id="fig:quarter_diffusion"/>. | ||
<figure id="fig:quarter_diffusion"> | <figure id="fig:quarter_diffusion"> | ||
| − | [[File:quarter_diffusion.png|thumb|upright=2|<caption>Example of solving using Neumann boundary conditions </caption>]] | + | [[File:quarter_diffusion.png|400px|thumb|upright=2|center|<caption>Example of solving using Neumann boundary conditions </caption>]] |
</figure> | </figure> | ||
Example code showing the use of Neumann boundary conditions: [https://gitlab.com/e62Lab/e62numcodes/blob/master/test/mlsm_operators_test.cpp example code] | Example code showing the use of Neumann boundary conditions: [https://gitlab.com/e62Lab/e62numcodes/blob/master/test/mlsm_operators_test.cpp example code] | ||
| − | We also support more -- interesting -- domains :) On <xr id="fig:mikimouse_heat"/> we see a | + | == Different geometries == |
| + | |||
| + | We also support more -- interesting -- domains :) On <xr id="fig:mikimouse_heat"/>, <xr id="fig:poisson_weird1"/> and <xr id="fig:poisson_weird2"/> we see a solution to $\triangle u = 1$ with zero boundary conditions on more interesting geometries. | ||
<figure id="fig:mikimouse_heat"> | <figure id="fig:mikimouse_heat"> | ||
| − | [[File:mikimouse_heat.png|thumb|upright=2| | + | [[File:mikimouse_heat.png|400px|thumb|upright=2|left|<caption>Miki mouse domain </caption>]] |
| + | </figure> | ||
| + | <figure id="fig:poisson_weird1"> | ||
| + | [[File:poisson_weird1.png|400px|thumb|upright=2|right|<caption>Domain 2</caption>]] | ||
| + | </figure> | ||
| + | <figure id="fig:poisson_weird2"> | ||
| + | [[File:poisson_weird2.png|200px|thumb|upright=2|center|<caption>Domain 3</caption>]] | ||
</figure> | </figure> | ||
| + | <!-- | ||
==Convergence analysis for one dimensional diffusion equation== | ==Convergence analysis for one dimensional diffusion equation== | ||
We now tried to solve the diffusion equation in one dimension | We now tried to solve the diffusion equation in one dimension | ||
| Line 136: | Line 167: | ||
<strong> Note: </strong> the results are <strong>not confirmed </strong> and serve merely as an orientation. Errors may have occured. | <strong> Note: </strong> the results are <strong>not confirmed </strong> and serve merely as an orientation. Errors may have occured. | ||
| − | + | ==Convergence with respect to number of nodes and support size== | |
Convergence of the method was tested on different number of nodes $N = 15, 20, 25, \ldots, 200$. First we tested the method, when support size is equal to number of monomials in the basis ($n =m$), which we call local interpolation, for different values of $n = 3, 5, 7$. We then compared that to local approximation, where we take $n = 12$ supporting nodes and we only change number of monomials. We used gaussian weight function with $\sigma = 1\cdot \Delta x$. Error was calculated after $0.001$ time units have elapsed. We can see the results on <xr id="fig:diffusionConvergence1d"/>. | Convergence of the method was tested on different number of nodes $N = 15, 20, 25, \ldots, 200$. First we tested the method, when support size is equal to number of monomials in the basis ($n =m$), which we call local interpolation, for different values of $n = 3, 5, 7$. We then compared that to local approximation, where we take $n = 12$ supporting nodes and we only change number of monomials. We used gaussian weight function with $\sigma = 1\cdot \Delta x$. Error was calculated after $0.001$ time units have elapsed. We can see the results on <xr id="fig:diffusionConvergence1d"/>. | ||
| Line 146: | Line 177: | ||
Larger is the support size, faster is convergence. This rule applies for local interpolation as well as approximation. But when number of nodes is too large, the method diverges faster for larger support sizes. Error for approximation is bigger than for interpolation (if we compare it for same basis size), but the method diverges with interpolation for smaller number of nodes. | Larger is the support size, faster is convergence. This rule applies for local interpolation as well as approximation. But when number of nodes is too large, the method diverges faster for larger support sizes. Error for approximation is bigger than for interpolation (if we compare it for same basis size), but the method diverges with interpolation for smaller number of nodes. | ||
| − | + | ==Convergence with respect to weight function== | |
We also checked the convergence for different weight functions. We tested it on number of nodes $N = 15, 20, 25, \ldots, 200$, with monomial basis with $m = 5$, support size $n = 12$ and gaussian weight function with $\sigma = w\cdot \Delta x$ for $w = 0.1$. Error was calculated after $0.001$ time units have elapsed with $\Delta t = 10^{-8}$. We can see the results on <xr id="fig:diffusionConvergence1dWeights"/>. | We also checked the convergence for different weight functions. We tested it on number of nodes $N = 15, 20, 25, \ldots, 200$, with monomial basis with $m = 5$, support size $n = 12$ and gaussian weight function with $\sigma = w\cdot \Delta x$ for $w = 0.1$. Error was calculated after $0.001$ time units have elapsed with $\Delta t = 10^{-8}$. We can see the results on <xr id="fig:diffusionConvergence1dWeights"/>. | ||
| Line 155: | Line 186: | ||
When the $\sigma$ is too small, other nodes on the support domain are not taken into consideration, so taking $n = 12$ or $n = 3$ would give the same results. However when $\sigma$ is too large, all the nodes on the support domain are contributing and there is no significant difference between different weight functions. | When the $\sigma$ is too small, other nodes on the support domain are not taken into consideration, so taking $n = 12$ or $n = 3$ would give the same results. However when $\sigma$ is too large, all the nodes on the support domain are contributing and there is no significant difference between different weight functions. | ||
| + | --> | ||
| − | + | = Solving Electrostatics = | |
This example is taken from the [http://www.freefem.org/ff++/ftp/freefem++doc.pdf FreeFem++ manual (page 235)]. | This example is taken from the [http://www.freefem.org/ff++/ftp/freefem++doc.pdf FreeFem++ manual (page 235)]. | ||
| Line 177: | Line 209: | ||
\end{equation} | \end{equation} | ||
| − | We now solve this equation for a circular enclosure with two rectangular holes. The boundary of the circular enclosure is held at constant potential 0 V. The two rectangular holes are held at constant potentials +1 V and -1 V, respectively. A coloured scatter plot is available in figure <xr id="fig:electro_statics"/>. | + | We now solve this equation for a circular enclosure with two rectangular holes. The boundary of the circular enclosure is held at constant potential $0$ V. The two rectangular holes are held at constant potentials $+1$ V and $-1$ V, respectively. A coloured scatter plot is available in figure <xr id="fig:electro_statics"/>. |
| + | |||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed"> '''Code for electrostatics problem''' | ||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | <syntaxhighlight lang="c++" line> | ||
| + | // domain parameters, size, support and monomial order | ||
| + | int domain_size = 3000; | ||
| + | size_t n = 15; | ||
| + | size_t m = 3; | ||
| + | |||
| + | double radius = 5.0; | ||
| + | double width = 0.3; | ||
| + | double height = 3.0; | ||
| + | |||
| + | // extra boundary labels | ||
| + | int LEFT = -10; | ||
| + | int RIGHT = -20; | ||
| + | |||
| + | // build circular domain | ||
| + | CircleDomain<Vec2d> domain({0,0},radius); | ||
| + | domain.fillUniformInterior(domain_size); | ||
| + | domain.fillUniformBoundaryWithStep(domain.characteristicDistance()); | ||
| + | |||
| + | // build left rectangle | ||
| + | RectangleDomain<Vec2d> left({-2-width,-height},{-2+width,height}); | ||
| + | left.fillUniformBoundaryWithStep(domain.characteristicDistance()); | ||
| + | left.types[left.types == BOUNDARY] = LEFT; | ||
| + | domain.subtract(left); | ||
| + | |||
| + | // build right rectangle | ||
| + | RectangleDomain<Vec2d> right({2-width,-height},{2+width,height}); | ||
| + | right.fillUniformBoundaryWithStep(domain.characteristicDistance()); | ||
| + | right.types[right.types == BOUNDARY] = RIGHT; | ||
| + | domain.subtract(right); | ||
| + | |||
| + | // relax domain and find supports | ||
| + | domain.relax(50, 1e-2, 1.0, 3, 1000); | ||
| + | domain.findSupport(n); | ||
| + | |||
| + | // get interior and boundary ranges | ||
| + | Range<int> interior = domain.types == INTERNAL; | ||
| + | Range<int> boundary = domain.types == BOUNDARY; | ||
| + | Range<int> leftrect = domain.types == LEFT; | ||
| + | Range<int> rightrect = domain.types == RIGHT; | ||
| + | |||
| + | // initialize unknown concentration field and right-hand side | ||
| + | VecXd phi(domain.size(),1); | ||
| + | VecXd RHS(domain.size(),1); | ||
| + | |||
| + | // initialize interior values (this is an important step) | ||
| + | RHS[interior] = 0.0; | ||
| + | |||
| + | // set dirichlet boundary conditions | ||
| + | RHS[boundary] = 0.0; | ||
| + | RHS[leftrect] = -1.0; | ||
| + | RHS[rightrect] = 1.0; | ||
| + | |||
| + | // prepare shape functions and laplacian | ||
| + | std::vector<Triplet<double>> l_coeff; | ||
| + | for (auto& c : interior) { | ||
| + | Range<Vec2d> supp_domain = domain.positions[domain.support[c]]; | ||
| + | EngineMLS<Vec2d, Monomials, Gaussians> MLS(m,supp_domain,pow(domain.characteristicDistance(),2)); | ||
| + | VecXd shape = MLS.getShapeAt(supp_domain[0], {{2, 0}}) + | ||
| + | MLS.getShapeAt(supp_domain[0], {{0, 2}}); | ||
| + | for (size_t i = 0; i < supp_domain.size(); ++i) { | ||
| + | l_coeff.emplace_back(c, domain.support[c][i], shape[i]); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | // prepare dirichlet boundaries | ||
| + | std::vector<Triplet<double>> b_coeff; | ||
| + | for (auto& c : domain.types < 0) { | ||
| + | b_coeff.emplace_back(c, c, 1.0); | ||
| + | } | ||
| + | |||
| + | // prepare matrices | ||
| + | SparseMatrix<double> laplace_m(domain.size(), domain.size()); | ||
| + | laplace_m.setFromTriplets(l_coeff.begin(), l_coeff.end()); | ||
| + | SparseMatrix<double> boundary_m(domain.size(), domain.size()); | ||
| + | boundary_m.setFromTriplets(b_coeff.begin(), b_coeff.end()); | ||
| + | |||
| + | // draw | ||
| + | std::thread th([&] { draw2D(domain.positions, phi); }); | ||
| + | |||
| + | // initialize solver | ||
| + | Eigen::BiCGSTAB<SparseMatrix<double>> solver; | ||
| + | |||
| + | // join matrices together | ||
| + | SparseMatrix<double> tmp = boundary_m + laplace_m; | ||
| + | solver.compute(tmp); | ||
| + | |||
| + | // solve system of equations | ||
| + | phi = solver.solve(RHS); | ||
| + | std::cout << "#iterations: " << solver.iterations() << std::endl; | ||
| + | std::cout << "estimated error: " << solver.error() << std::endl; | ||
| + | |||
| + | // end drawing | ||
| + | th.join(); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
<figure id="fig:electro_statics"> | <figure id="fig:electro_statics"> | ||
| − | [[File: | + | [[File:electrostatics.png|thumb|upright=2|center|<caption> Simple electrostatics problem solved by implicit method with 15 node monomial supports and gaussian weight functions. </caption>]] |
| + | </figure> | ||
| + | |||
| + | = Convection-diffusion = | ||
| + | |||
| + | The following example problem is adapted from [http://servidor.demec.ufpr.br/CFD/bibliografia/Ferziger%20Peric%20-%20Computational%20Methods%20for%20Fluid%20Dynamics,%203rd%20Ed%20-%202002.pdf Ferziger & Perič (2002) (pages 82-86)]. | ||
| + | |||
| + | <figure id="fig:fvm_problem"> | ||
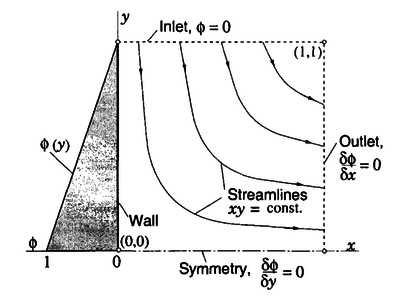
| + | [[File:Screenshot_2016-11-28_11-05-03.png|thumb|400px|upright=2|centre|<caption> Geometry and boundary conditions for the scalar transport in a stagnation point flow. </caption>]] | ||
| + | </figure> | ||
| + | |||
| + | We now consider the problem of a scalar quantity transported in a known velocity field $\b{u}$. The velocity field is given by | ||
| + | \[\b{u} = (u_x,u_y) = (x, -y),\] | ||
| + | which represents the flow near a stagnation point $(x,y) = (0,0)$. The streamlines $xy=\mathrm{const.}$ and change direction with respect to the Cartesian grid. The convection-diffusion equation (also known as the scalar transport equation) to be solved is | ||
| + | \[\alpha \b{\nabla}^2 \phi - \b{u}\cdot \b{\nabla}\phi = 0\] | ||
| + | with the following boundary conditions: | ||
| + | * $\phi = 0$ along the north (inlet) boundary; | ||
| + | * linear variation $\phi = (1 - y)$ along the west boundary ($x = 0$); | ||
| + | * symmetry condition on the south boundary; | ||
| + | * zero gradient at the east (outlet) boundary. | ||
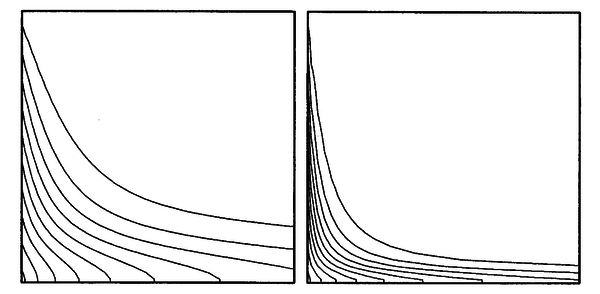
| + | The parameter $\alpha$ is the diffusivity for the scalar quantity $\phi$. The problem and boundary conditions are schematically represented in the <xr id="fig:fvm_problem"/>. The solutions obtained by Ferziger and Perić are shown in <xr id="fig:fvm_problem_solution"/>. | ||
| + | |||
| + | <figure id="fig:fvm_problem_solution"> | ||
| + | [[File:Screenshot_2016-11-28_11-07-44.png|thumb|600px|center|upright=2|<caption> Isolines of $\phi$, from 0.05 to 0.95 with step 0.1 (top to bottom), for $\alpha = 0.01$ (left) and $\alpha = 0.001$ (right). </caption>]] | ||
| + | </figure> | ||
| + | |||
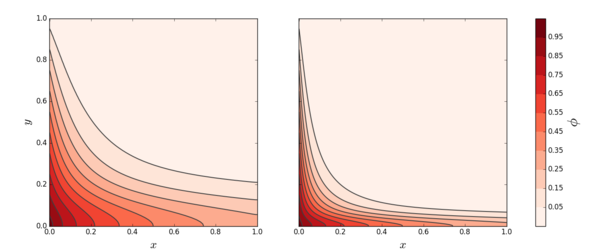
| + | The meshless solution is obtained on regular point arrangements of sizes 100 × 100 and 300 × 300, for the 2 cases of diffusivity $\alpha = 0.01$ and $\alpha = 0.001$, respectively. For comparison we have plotted the contour lines at the same intervals as the original authors of this example (see <xr id="fig:fvm_problem_meshless"/>). The basis functions are the 5 monomials $1$, $x$, $y$, $x^2$, $y^2$. | ||
| + | |||
| + | <figure id="fig:fvm_problem_meshless"> | ||
| + | [[File:fvm_convection.png|thumb|600px|center|upright=2|<caption> Isolines of $\phi$, from 0.05 to 0.95 with step 0.1 (top to bottom), for $\alpha = 0.01$ (left) and $\alpha = 0.001$ (right), obtaines with meshless solver. </caption>]] | ||
</figure> | </figure> | ||
Latest revision as of 19:36, 6 October 2017
Solving Diffusion equation
For starters, we can solve simple Diffusion equation $ \nabla^2 u = \frac{\partial u}{\partial t} $.
We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and initial state $ u(t = 0) = 1$.
An analytical solution for this domain is known, and we use it to evaluate or own solution. \begin{equation} u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} \end{equation} Because the solution is given in the series form, we only compare to the finite approximation, summing to $N = 100$ instead of infinity. Solution is on Figure 1. See the code for solving diffusion here.
Convergence with respect to number of nodes
We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ on a unit square ($a = 1$). Results are on Figure 2. Monomial basis of $6$ monomials was used and $12$ closest nodes counted as support for each node. After more than $250$ nodes of discretization in each dimension the method diverges, which is expected. The stability criterion for diffusion equation in two dimensions is $\Delta t \leq \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization step in one dimension. In our case, at $250$ nodes per side, the right hand side yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, so our method is stable within the expected region.
On Figure 3 is another image of convergence, this time using monomial basis $\{1, x, y, x^2, y^2\}$ and Gaussian basis with discretization step $ \Delta t = 5 \cdot 10^{-6}$ and 5 support nodes. Total node count was $N = 2500$. Error was calculated after $0.01$ time units have elapsed.
Figure 4 shows convergence of 1/4 of the whole solution with Dirichlet boundary conditions (Fig. 1). The nodes were spanning the area $[0, a/2]^2$. As expected, higher number of nodes yields lower max error up to some maximal number of nodes. The latter is lower for explicit than for implicit method.
Convergence with respect to number of time steps
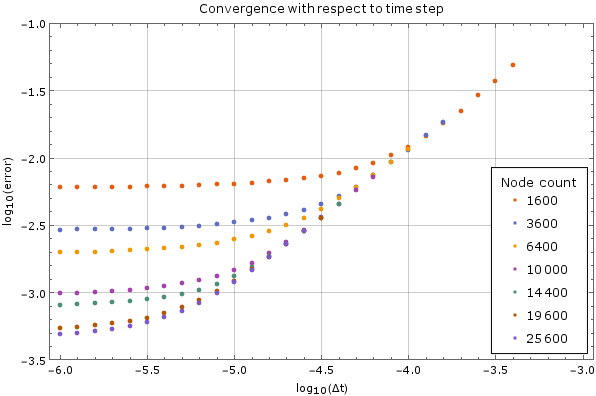
We tested the method on a fixed node count with different time steps on the same domain as above. Results are on Figure 5. For large time steps the method diverges, but once it starts converging the precision increases steadily as the time step decreases, until it hits its lower limit. This behaviour is expected. The error was calculated against the analytical solution above after $0.005$ units of time have passed. A monomial basis up to order $2$ inclusive ($m = 6$) was used and the support size was $n = 12$.
Using Gaussian basis
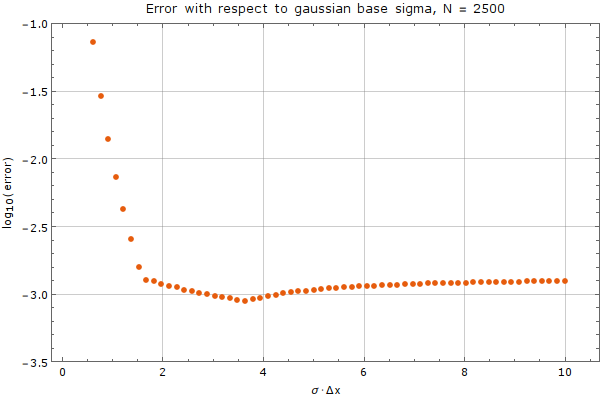
We tested the method on a fixed node count of $N = 2500$ with spatial step discretization of $\Delta x = \frac{1}{50}$. We used the Gaussian basis of $m = 5$ functions with support size $n = 13$. Error was calculated against analytical solution above after $0.01$ time units. A time step of $\Delta t = 10^{-5}$ was used. Results are on Figure 6
As we can see from the graph, there exists an interval where the choice of $\sigma$ does not matter much, but outside of this interval, the method diverges rapidly. Care from the user side must be taken, to choose $\sigma$ appropriately, with respect to plot above.
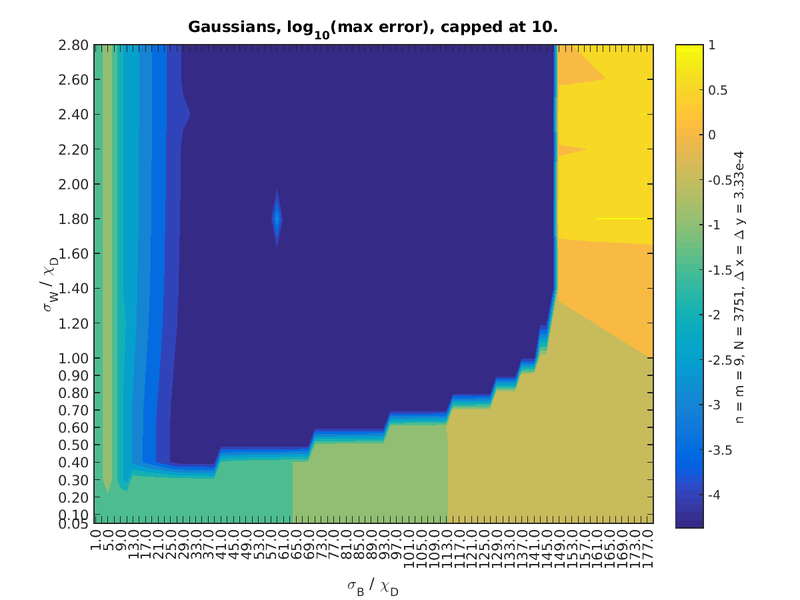
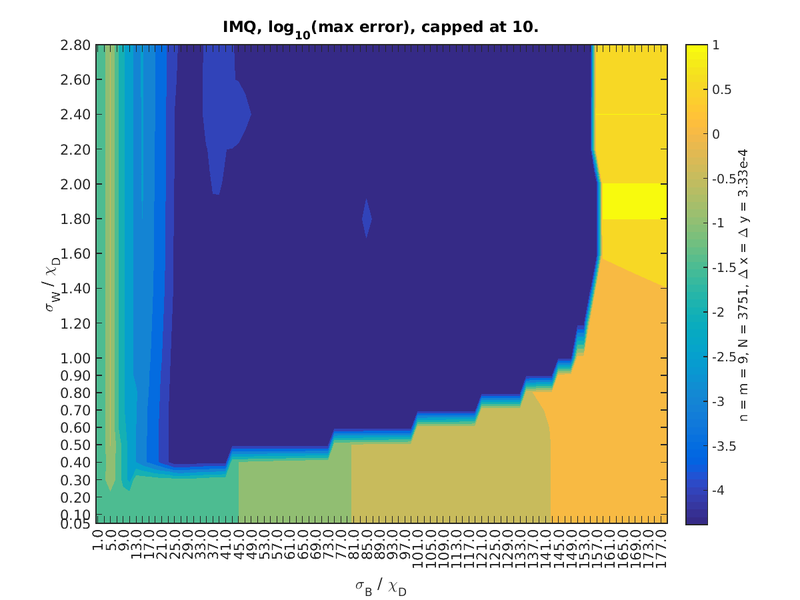
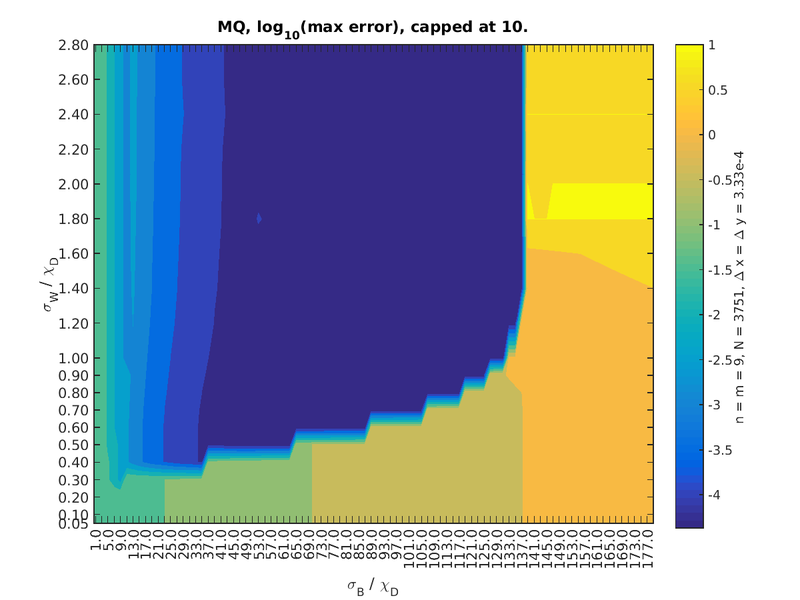
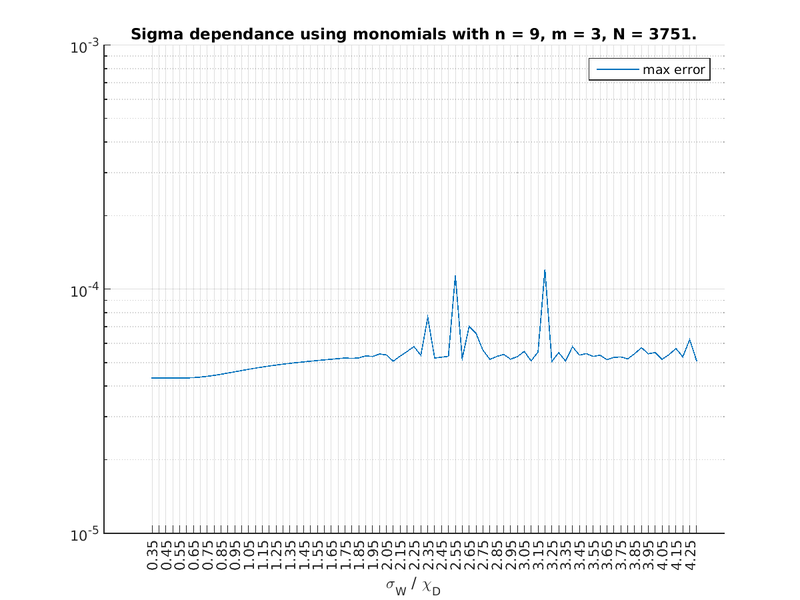
Convergence with respect to shape parameters
Choice of shape of the basis function can have significant effect on solution of the system. We tested the space of feasible shape parameters on the diffusion equation with $\Delta x = \Delta y = 0.01$ and $m = n = 9$. The weight function does not have much influence here, except on the condition number and any singular values that get cut off because of that.
Results for Gaussian, MQ and IMQ basis functions are presented in Figure 7, Figure 8 and Figure 10.
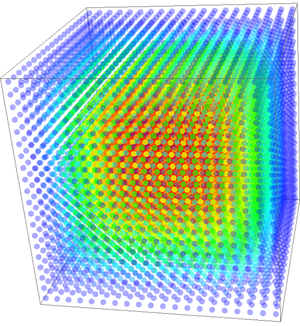
Solving in 3D
A 3-dimensional case on domain $[0, 1]^3$ was tested on $N = 20^3$ nodes, making the discretization step $\Delta x = 0.05$. Support size of $n=10$ with $m=10$ Gaussian basis functions was used. Their normalization parameter was $\sigma = 60\Delta x$. A time step of $\Delta t = 10^{-5}$ and an explicit Euler method was used to calculate the solution of to $0.01$ time units. Resulting function is on Figure 11.
Solving mixed boundary conditions with MLSM operators
By using MLSM operators and utilizing its `MLSM::neumann` method we can also solve partial diffusion equations. Solution is on Figure 12.
Example code showing the use of Neumann boundary conditions: example code
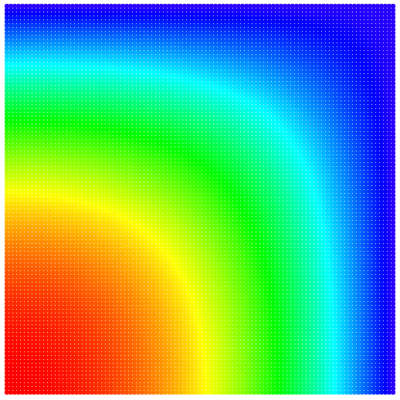
Different geometries
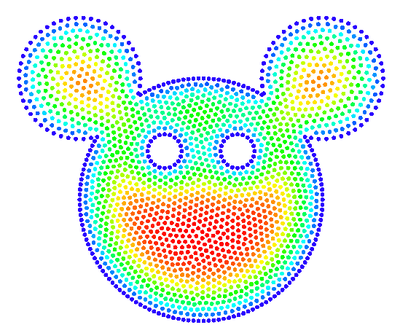
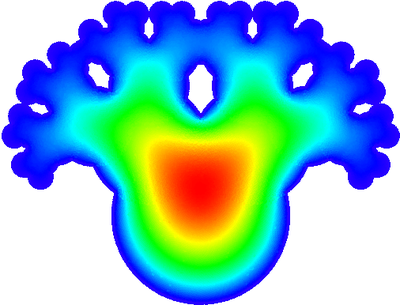
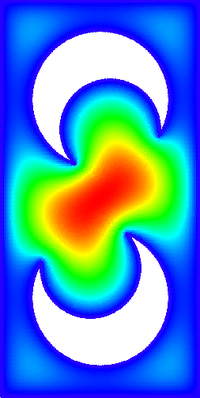
We also support more -- interesting -- domains :) On Figure 13, Figure 14 and Figure 15 we see a solution to $\triangle u = 1$ with zero boundary conditions on more interesting geometries.
Solving Electrostatics
This example is taken from the FreeFem++ manual (page 235).
Assuming there is no current and the charge distribution is time independent, the electric field $\b{E}$ satisfies \begin{equation}\label{eq:electrostatics} \b{\nabla}\cdot\b{E} = \frac{\rho}{\epsilon}, \quad \b{\nabla} \times \b{E} = 0 \end{equation} where $\rho$ is the charge density and $\epsilon$ is the permittivity. If we introduce an electrostatics potential $\phi$ such that \begin{equation} \b{E} = -\b{\nabla}\phi, \end{equation} we can insert it into the first equation in (\ref{eq:electrostatics}) resulting in Poisson's equation \begin{equation}\label{eq:poisson} \b{\nabla}^2 \phi = -\frac{\rho}{\epsilon}. \end{equation} In the absence of unpaired electric charge equation (\ref{eq:poisson}) becomes Laplace's equation \begin{equation} \b{\nabla}^2 \phi = 0 \end{equation}
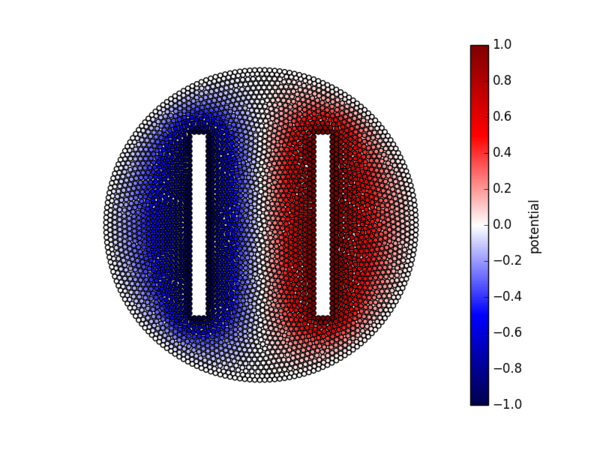
We now solve this equation for a circular enclosure with two rectangular holes. The boundary of the circular enclosure is held at constant potential $0$ V. The two rectangular holes are held at constant potentials $+1$ V and $-1$ V, respectively. A coloured scatter plot is available in figure Figure 16.
1 // domain parameters, size, support and monomial order
2 int domain_size = 3000;
3 size_t n = 15;
4 size_t m = 3;
5
6 double radius = 5.0;
7 double width = 0.3;
8 double height = 3.0;
9
10 // extra boundary labels
11 int LEFT = -10;
12 int RIGHT = -20;
13
14 // build circular domain
15 CircleDomain<Vec2d> domain({0,0},radius);
16 domain.fillUniformInterior(domain_size);
17 domain.fillUniformBoundaryWithStep(domain.characteristicDistance());
18
19 // build left rectangle
20 RectangleDomain<Vec2d> left({-2-width,-height},{-2+width,height});
21 left.fillUniformBoundaryWithStep(domain.characteristicDistance());
22 left.types[left.types == BOUNDARY] = LEFT;
23 domain.subtract(left);
24
25 // build right rectangle
26 RectangleDomain<Vec2d> right({2-width,-height},{2+width,height});
27 right.fillUniformBoundaryWithStep(domain.characteristicDistance());
28 right.types[right.types == BOUNDARY] = RIGHT;
29 domain.subtract(right);
30
31 // relax domain and find supports
32 domain.relax(50, 1e-2, 1.0, 3, 1000);
33 domain.findSupport(n);
34
35 // get interior and boundary ranges
36 Range<int> interior = domain.types == INTERNAL;
37 Range<int> boundary = domain.types == BOUNDARY;
38 Range<int> leftrect = domain.types == LEFT;
39 Range<int> rightrect = domain.types == RIGHT;
40
41 // initialize unknown concentration field and right-hand side
42 VecXd phi(domain.size(),1);
43 VecXd RHS(domain.size(),1);
44
45 // initialize interior values (this is an important step)
46 RHS[interior] = 0.0;
47
48 // set dirichlet boundary conditions
49 RHS[boundary] = 0.0;
50 RHS[leftrect] = -1.0;
51 RHS[rightrect] = 1.0;
52
53 // prepare shape functions and laplacian
54 std::vector<Triplet<double>> l_coeff;
55 for (auto& c : interior) {
56 Range<Vec2d> supp_domain = domain.positions[domain.support[c]];
57 EngineMLS<Vec2d, Monomials, Gaussians> MLS(m,supp_domain,pow(domain.characteristicDistance(),2));
58 VecXd shape = MLS.getShapeAt(supp_domain[0], {{2, 0}}) +
59 MLS.getShapeAt(supp_domain[0], {{0, 2}});
60 for (size_t i = 0; i < supp_domain.size(); ++i) {
61 l_coeff.emplace_back(c, domain.support[c][i], shape[i]);
62 }
63 }
64
65 // prepare dirichlet boundaries
66 std::vector<Triplet<double>> b_coeff;
67 for (auto& c : domain.types < 0) {
68 b_coeff.emplace_back(c, c, 1.0);
69 }
70
71 // prepare matrices
72 SparseMatrix<double> laplace_m(domain.size(), domain.size());
73 laplace_m.setFromTriplets(l_coeff.begin(), l_coeff.end());
74 SparseMatrix<double> boundary_m(domain.size(), domain.size());
75 boundary_m.setFromTriplets(b_coeff.begin(), b_coeff.end());
76
77 // draw
78 std::thread th([&] { draw2D(domain.positions, phi); });
79
80 // initialize solver
81 Eigen::BiCGSTAB<SparseMatrix<double>> solver;
82
83 // join matrices together
84 SparseMatrix<double> tmp = boundary_m + laplace_m;
85 solver.compute(tmp);
86
87 // solve system of equations
88 phi = solver.solve(RHS);
89 std::cout << "#iterations: " << solver.iterations() << std::endl;
90 std::cout << "estimated error: " << solver.error() << std::endl;
91
92 // end drawing
93 th.join();
Convection-diffusion
The following example problem is adapted from Ferziger & Perič (2002) (pages 82-86).
We now consider the problem of a scalar quantity transported in a known velocity field $\b{u}$. The velocity field is given by \[\b{u} = (u_x,u_y) = (x, -y),\] which represents the flow near a stagnation point $(x,y) = (0,0)$. The streamlines $xy=\mathrm{const.}$ and change direction with respect to the Cartesian grid. The convection-diffusion equation (also known as the scalar transport equation) to be solved is \[\alpha \b{\nabla}^2 \phi - \b{u}\cdot \b{\nabla}\phi = 0\] with the following boundary conditions:
- $\phi = 0$ along the north (inlet) boundary;
- linear variation $\phi = (1 - y)$ along the west boundary ($x = 0$);
- symmetry condition on the south boundary;
- zero gradient at the east (outlet) boundary.
The parameter $\alpha$ is the diffusivity for the scalar quantity $\phi$. The problem and boundary conditions are schematically represented in the Figure 17. The solutions obtained by Ferziger and Perić are shown in Figure 18.
The meshless solution is obtained on regular point arrangements of sizes 100 × 100 and 300 × 300, for the 2 cases of diffusivity $\alpha = 0.01$ and $\alpha = 0.001$, respectively. For comparison we have plotted the contour lines at the same intervals as the original authors of this example (see Figure 19). The basis functions are the 5 monomials $1$, $x$, $y$, $x^2$, $y^2$.