Difference between revisions of "Natural convection in 3D irregular domain"

From Medusa: Coordinate Free Mehless Method implementation
Jump to: navigation, search
 
(18 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
The classical [[De Vahl Davis natural convection test]] can be extended to 3D []
+
The classical [[De Vahl Davis natural convection test]] can be extended to 3D.
−
 
+
In below figures steady state temperature contour and velocity quiver plots
 +
for Ra$=10^6$ case in 3D are presented. A more quantitative analysis is done by comparing characteristic values, i.e.
 +
peak positions and values of cross section velocities, with data available in literature. We analyze six different cases,
 +
namely Ra$=10^6,10^7,10^8$ in 2D, and Ra$=10^4,10^5,10^6$ in 3D.
 +
The comparison in presented in below table.
  
 
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis
 
All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis
 
functions, augmented with monomials up to order $2$, with the closest $25$
 
functions, augmented with monomials up to order $2$, with the closest $25$
 
nodes used as a stencil. For the time discretization time step
 
nodes used as a stencil. For the time discretization time step
−
$\Delta t=10^{-3}$ was used for all cases. Nodal distance $h=0.01$ is used for
+
$\Delta t=10^{-3}$ was used for all cases. Domain is discretized with our [[Positioning of computational nodes|fill algoritm]] with
−
simulations in 2D and $h=0.25$ for simulations in 3D. Boundaries with Neumann
+
Nodal distance $h=0.025$. Boundaries with Neumann
−
boundary conditions are additionally treated with ghost nodes [[Ghost nodes (theory)]].
+
boundary conditions are additionally treated with [[Ghost nodes (theory)]].
 +
 
 +
[[File:DVD_3D.png|400px]]
 +
[[File:DVD_3D_irreg.png|400px]]
 +
 
 +
{| class="wikitable"
 +
!
 +
! style="text-align: center;" | Ra
 +
! $v_{max}$
 +
!
 +
!
 +
! $x$
 +
!
 +
!
 +
! $u_{max}$
 +
!
 +
!
 +
! $y$
 +
!
 +
!
 +
|-
 +
|
 +
|
 +
| present
 +
| ref a
 +
| ref b
 +
| present
 +
| ref a
 +
| ref b
 +
| present
 +
| ref a
 +
| ref b
 +
| present
 +
| ref a
 +
| ref b
 +
|-
 +
| 2D
 +
| $10^6$
 +
| 0.2628
 +
| 0.2604
 +
| 0.2627
 +
| 0.0378
 +
| 0.0380
 +
| 0.0390
 +
| 0.0781
 +
| 0.0765
 +
| 0.0782
 +
| 0.8476
 +
| 0.8510
 +
| 0.0390
 +
|-
 +
|
 +
| $10^7$
 +
| 0.2633
 +
| 0.2580
 +
| 0.2579
 +
| 0.0226
 +
| 0.0230
 +
| 0.0210
 +
| 0.0588
 +
| 0.0547
 +
| 0.0561
 +
| 0.8705
 +
| 0.8880
 +
| 0.0210
 +
|-
 +
|
 +
| $10^8$
 +
| 0.2557
 +
| 0.2587
 +
| 0.2487
 +
| 0.0149
 +
| 0.0110
 +
| 0.0090
 +
| 0.0314
 +
| 0.0379
 +
| 0.0331
 +
| 0.9189
 +
| 0.9430
 +
| 0.0090
 +
|-
 +
| 3D
 +
| $10^4$
 +
| 0.2495
 +
| 0.2218
 +
| 0.2252
 +
| 0.8500
 +
| 0.8873
 +
| 0.8833
 +
| 0.2435
 +
| 0.1968
 +
| 0.2013
 +
| 0.1611
 +
| 0.1799
 +
| 0.1833
 +
|-
 +
|
 +
| $10^5$
 +
| 0.2545
 +
| 0.2442
 +
| 0.2471
 +
| 0.9402
 +
| 0.9317
 +
| 0.9353
 +
| 0.1564
 +
| 0.1426
 +
| 0.1468
 +
| 0.1447
 +
| 0.1493
 +
| 0.1453
 +
|-
 +
|
 +
| $10^6$
 +
| 0.2564
 +
| 0.2556
 +
| 0.2588
 +
| 0.9614
 +
| 0.9653
 +
| 0.9669
 +
| 0.0841
 +
| 0.0816
 +
| 0.0841
 +
| 0.1435
 +
| 0.1403
 +
| 0.1443
 +
|}
 +
 
 +
[ref a for 2D] Couturier, H. & Sadat, S. Performance and accuracy of a meshless method for laminar natural convection Numerical Heat Transfer: Part B: Fundamentals, Taylor & Francis, 2000 , 37 , 455-467
  
−
[[File:DVD_3D_irreg.png|400px]][[File:DVD_3D.png|400px]]
+
[ref b for 2D] Kosec, G. & Šarler, B. Solution of thermo-fluid problems by collocation with local pressure correction International Journal of Numerical Methods for Heat & Fluid Flow, Emerald Group Publishing Limited, 2008 , 18 , 868-882
  
 +
[ref a for 3D] Wang, P.; Zhang, Y. & Guo, Z. Numerical study of three-dimensional natural convection in a cubical cavity at high Rayleigh numbers Int. J. Heat Mass Transfer, Elsevier, 2017 , 113 , 217-228
  
−
\begin{table}[h]
+
[ref b for 3D] Fusegi, T.; Hyun, J. M.; Kuwahara, K. & Farouk, B. A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure Int. J. Heat Mass Transfer, Elsevier, 1991 , 34 , 1543-1557
−
  \centering
 
−
  \caption{Comparison of results computed with RBF-FD on FF nodes and reference
 
−
  data. }
 
−
  \label{tab:ff-data}
 
−
  \renewcommand{\arraystretch}{1.2}
 
−
  \scalebox{0.68}{
 
−
  \begin{tabular}{|l|l|l|l|l|l|l|l|l|l|l|l|l|l|}
 
−
    \cline{2-14}
 
−
      \multicolumn{1}{c|}{} & \multirow{2}{*}{\textbf{Ra}} &
 
−
      \multicolumn{3}{c|}{$v_{max}(x, 0.5)$} & \multicolumn{3}{c|}{$x$}  &
 
−
      \multicolumn{3}{c|}{$u_{max}(0.5, y)$} & \multicolumn{3}{c|}{$y$}
 
−
    \\ \cline{3-14}
 
−
      \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{} & present &
 
−
      \multicolumn{1}{c|}{\cite{couturier2000performance}} &
 
−
      \multicolumn{1}{c|}{\cite{kosec2008solution}} & present &
 
−
      \multicolumn{1}{c|}{\cite{couturier2000performance}} &
 
−
      \multicolumn{1}{c|}{\cite{kosec2008solution}} & present &
 
−
      \multicolumn{1}{c|}{\cite{couturier2000performance}} &
 
−
      \multicolumn{1}{c|}{\cite{kosec2008solution}} & present &
 
−
      \multicolumn{1}{c|}{\cite{couturier2000performance}} &
 
−
      \multicolumn{1}{c|}{\cite{kosec2008solution}}
 
−
    \\ \hline \hline
 
−
      \multirow{3}{*}{\textbf{2D}} & $10^6$ & 0.2628    & 0.2604  &
 
−
      0.2627  & 0.037  & 0.038 & 0.039 & 0.0781    & 0.0765  & 0.0782  & 0.847
 
−
      & 0.851 & 0.861
 
−
    \\ \cline{2-14}
 
−
      & $10^7$ & 0.2633    & 0.2580  & 0.2579  & 0.022  & 0.023 & 0.021 & 0.0588
 
−
      & 0.0547  & 0.0561 & 0.870  & 0.888 & 0.900
 
−
    \\ \cline{2-14}
 
−
      & $10^8$ & 0.2557    & 0.2587  & 0.2487  & 0.010  & 0.011 & 0.009 & 0.0314
 
−
      & 0.0379  & 0.0331  & 0.918  & 0.943 & 0.930
 
−
    \\ \hline \hline
 
−
      \multicolumn{1}{c|}{} & \multirow{2}{*}{\textbf{Ra}} &
 
−
      \multicolumn{3}{c|}{$w_{max}(x, 0.5,0.5)$} & \multicolumn{3}{c|}{$x$}  &
 
−
      \multicolumn{3}{c|}{$u_{max}(0.5, 0.5, z)$} & \multicolumn{3}{c|}{$z$}
 
−
    \\ \cline{3-14}
 
−
      \multicolumn{1}{c|}{} & \multicolumn{1}{c|}{} & present &
 
−
      \multicolumn{1}{c|}{\cite{wang2017numerical}}
 
−
      & \multicolumn{1}{c|}{\cite{fusegi1991numerical}} & present &
 
−
      \multicolumn{1}{c|}{\cite{wang2017numerical}}
 
−
      & \multicolumn{1}{c|}{\cite{fusegi1991numerical}} & present &
 
−
      \multicolumn{1}{c|}{\cite{wang2017numerical}}
 
−
      & \multicolumn{1}{c|}{\cite{fusegi1991numerical}} & present &
 
−
      \multicolumn{1}{c|}{\cite{wang2017numerical}} &
 
−
      \multicolumn{1}{c|}{\cite{fusegi1991numerical}}
 
−
    \\  \hline
 
−
      \multirow{3}{*}{\textbf{3D}} & $10^4$ & 0.2295 & 0.2218  & 0.2252  & 0.850 & 0.887 & 0.883
 
−
      & 0.2135    & 0.1968  & 0.2013  & 0.168 & 0.179 & 0.183 \\ \cline{2-14}
 
−
      & $10^5$ & 0.2545    & 0.2442  & 0.2471  & 0.940  & 0.931 & 0.935 & 0.1564 & 0.1426 & 0.1468
 
−
      & 0.144  & 0.149 & 0.145
 
−
    \\ \cline{2-14}
 
−
      & $10^6$ & 0.2564 & 0.2556 & 0.2588 & 0.961  & 0.965 & 0.966 & 0.0841
 
−
      & 0.0816  & 0.0841 & 0.143 & 0.140 & 0.144
 
−
    \\ \hline
 
−
  \end{tabular}
 
−
  }
 
−
\end{table}
 

Latest revision as of 16:03, 18 May 2019

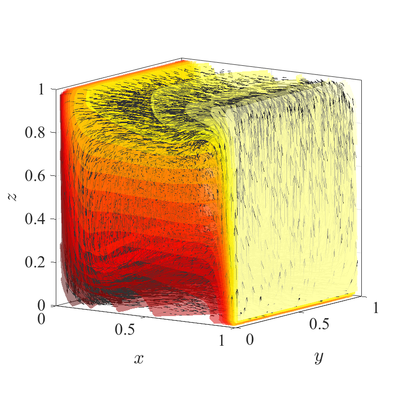
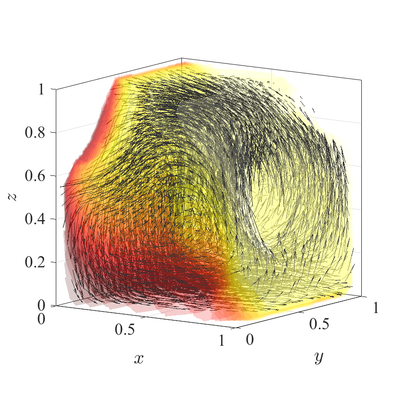
The classical De Vahl Davis natural convection test can be extended to 3D. In below figures steady state temperature contour and velocity quiver plots for Ra$=10^6$ case in 3D are presented. A more quantitative analysis is done by comparing characteristic values, i.e. peak positions and values of cross section velocities, with data available in literature. We analyze six different cases, namely Ra$=10^6,10^7,10^8$ in 2D, and Ra$=10^4,10^5,10^6$ in 3D. The comparison in presented in below table.

All spatial operators are discretized using RBF-FD with $r^3$ PHS radial basis functions, augmented with monomials up to order $2$, with the closest $25$ nodes used as a stencil. For the time discretization time step $\Delta t=10^{-3}$ was used for all cases. Domain is discretized with our fill algoritm with Nodal distance $h=0.025$. Boundaries with Neumann boundary conditions are additionally treated with Ghost nodes (theory).

DVD 3D.png DVD 3D irreg.png

Ra $v_{max}$ $x$ $u_{max}$ $y$
present ref a ref b present ref a ref b present ref a ref b present ref a ref b
2D $10^6$ 0.2628 0.2604 0.2627 0.0378 0.0380 0.0390 0.0781 0.0765 0.0782 0.8476 0.8510 0.0390
$10^7$ 0.2633 0.2580 0.2579 0.0226 0.0230 0.0210 0.0588 0.0547 0.0561 0.8705 0.8880 0.0210
$10^8$ 0.2557 0.2587 0.2487 0.0149 0.0110 0.0090 0.0314 0.0379 0.0331 0.9189 0.9430 0.0090
3D $10^4$ 0.2495 0.2218 0.2252 0.8500 0.8873 0.8833 0.2435 0.1968 0.2013 0.1611 0.1799 0.1833
$10^5$ 0.2545 0.2442 0.2471 0.9402 0.9317 0.9353 0.1564 0.1426 0.1468 0.1447 0.1493 0.1453
$10^6$ 0.2564 0.2556 0.2588 0.9614 0.9653 0.9669 0.0841 0.0816 0.0841 0.1435 0.1403 0.1443

[ref a for 2D] Couturier, H. & Sadat, S. Performance and accuracy of a meshless method for laminar natural convection Numerical Heat Transfer: Part B: Fundamentals, Taylor & Francis, 2000 , 37 , 455-467

[ref b for 2D] Kosec, G. & Šarler, B. Solution of thermo-fluid problems by collocation with local pressure correction International Journal of Numerical Methods for Heat & Fluid Flow, Emerald Group Publishing Limited, 2008 , 18 , 868-882

[ref a for 3D] Wang, P.; Zhang, Y. & Guo, Z. Numerical study of three-dimensional natural convection in a cubical cavity at high Rayleigh numbers Int. J. Heat Mass Transfer, Elsevier, 2017 , 113 , 217-228

[ref b for 3D] Fusegi, T.; Hyun, J. M.; Kuwahara, K. & Farouk, B. A numerical study of three-dimensional natural convection in a differentially heated cubical enclosure Int. J. Heat Mass Transfer, Elsevier, 1991 , 34 , 1543-1557

Retrieved from "http://e6.ijs.si/medusa/wiki/index.php?title=Natural_convection_in_3D_irregular_domain&oldid=2533"