Difference between revisions of "Natural convection from heated cylinder"

From Medusa: Coordinate Free Mehless Method implementation
Jump to: navigation, search
 
(9 intermediate revisions by one other user not shown)
Line 1: Line 1:
 +
{{Box-round|title= Related papers |
 +
[https://e6.ijs.si/ParallelAndDistributedSystems/publications/32388135.pdf M. Maksić, V. Djurica, A. Souvent, J. Slak, M. Depolli, G. Kosec; Cooling of overhead power lines due to the natural convection, International journal of electrical power & energy systems, 2019]
 +
}}
 +
 +
 
Natural convection from a horizontal cylinder plays a crucial role in many heat transfer related problems ranging from heat exchangers, solar heating systems, cooling of electronic packages, to cooling of overhead power lines. One of the first studies of convective heat transfer from circular cylinders goes back to 1892 when Ayrton and Kilgour investigated the thermal emission of thin, long horizontal wires [1]. Several similar experiments followed [2], and in 1975 Morgan collected experimental data in a comprehensive review paper [3]. Based on the collected data Morgan introduced the correlations between Grashof, Prandtl and Nusselt numbers [3]. In other words, he presented relationships between the power of cooling in dependence on the material properties and the temperature difference between the cylinder and the ambient, which still serve as a basis in operative models for predicting the temperature of overhead power lines [4, 5]. There are many other similar studies where authors investigate the heat transfer from the heated cylinder due to the natural or forced convection under different conditions [2, 6, 7]. Benchmark case for the natural convection around the homogeneously heated cylinder was introduced in 1992 by Demirdžić, et al. [8]. The governing equations are the same as in [[De Vahl Davis natural convection test]].  
 
Natural convection from a horizontal cylinder plays a crucial role in many heat transfer related problems ranging from heat exchangers, solar heating systems, cooling of electronic packages, to cooling of overhead power lines. One of the first studies of convective heat transfer from circular cylinders goes back to 1892 when Ayrton and Kilgour investigated the thermal emission of thin, long horizontal wires [1]. Several similar experiments followed [2], and in 1975 Morgan collected experimental data in a comprehensive review paper [3]. Based on the collected data Morgan introduced the correlations between Grashof, Prandtl and Nusselt numbers [3]. In other words, he presented relationships between the power of cooling in dependence on the material properties and the temperature difference between the cylinder and the ambient, which still serve as a basis in operative models for predicting the temperature of overhead power lines [4, 5]. There are many other similar studies where authors investigate the heat transfer from the heated cylinder due to the natural or forced convection under different conditions [2, 6, 7]. Benchmark case for the natural convection around the homogeneously heated cylinder was introduced in 1992 by Demirdžić, et al. [8]. The governing equations are the same as in [[De Vahl Davis natural convection test]].  
  
Line 5: Line 10:
 
If we change boundary conditions in Demirdžić case we can also simulate cooling of overhead power line by natural convection. The problem is very similar to the previous one, with the main difference in a top boundary condition, where instead of confined cavity an open domain is assumed. Besides, the thermo-physical properties of real materials are considered and not dimensionless characterisation as in previous two examples. The power line 490-AL1/64-ST1A with radius 1.33 cm is positioned in the centre of in 5x5 cm square domain, and the air is modelled with following properties: $\rho =1.29\,\text{kg/}{{\text{m}}^{\text{3}}}$, ${{c}_{p}}=1005\,\text{J/kgK}$, $\beta=0.00367$, thermal conductivity modelled as ${{\lambda }_{a}}=2.368\cdot {{10}^{-2}}+7.23\cdot {{10}^{-5}}{{T}^{{}}}-2.763\cdot {{10}^{-8}}{{T}^{2}}\,\left[ \frac{\text{W}}{\text{mK}} \right]$ and viscosity modelled as
 
If we change boundary conditions in Demirdžić case we can also simulate cooling of overhead power line by natural convection. The problem is very similar to the previous one, with the main difference in a top boundary condition, where instead of confined cavity an open domain is assumed. Besides, the thermo-physical properties of real materials are considered and not dimensionless characterisation as in previous two examples. The power line 490-AL1/64-ST1A with radius 1.33 cm is positioned in the centre of in 5x5 cm square domain, and the air is modelled with following properties: $\rho =1.29\,\text{kg/}{{\text{m}}^{\text{3}}}$, ${{c}_{p}}=1005\,\text{J/kgK}$, $\beta=0.00367$, thermal conductivity modelled as ${{\lambda }_{a}}=2.368\cdot {{10}^{-2}}+7.23\cdot {{10}^{-5}}{{T}^{{}}}-2.763\cdot {{10}^{-8}}{{T}^{2}}\,\left[ \frac{\text{W}}{\text{mK}} \right]$ and viscosity modelled as
 
$\mu =\left( 17.239+4.635\cdot {{10}^{-2}}T-2.03\cdot {{10}^{-5}}{{T}^{2}} \right)\cdot {{10}^{-6}}\left[ \text{Pa}\,\text{s} \right]$.
 
$\mu =\left( 17.239+4.635\cdot {{10}^{-2}}T-2.03\cdot {{10}^{-5}}{{T}^{2}} \right)\cdot {{10}^{-6}}\left[ \text{Pa}\,\text{s} \right]$.
−
First, the temperature and velocity magnitude contour plots for ${{T}_{C}}={{0}^{{}^\circ }}\, \text{C}$ ${{T}_{H}}={{80}^{{}^\circ }}\,\text{C}$ are presented. In a next analysis we compare the power of convective cooling computed by presented MLSM solution procedure against two leading standards, namely CIGRE [4] and IEEE [5]. Although the agreement is not perfect, we are satisfied with the results. It is essential to understand that CIGRE and IEEE computations rely only on empirical relations, while the MLSM solution uses solely physical model and thermo-physical properties of air.
 
−
 
  
 
<figure id="fig:f1">
 
<figure id="fig:f1">
 
[[File:problem_scheme.png|600px]]
 
[[File:problem_scheme.png|600px]]
 
<caption>Scheme of the natural convection from heated cylinder cases. Left Demirdžić case and right cooling of overhead line case.</caption>
 
<caption>Scheme of the natural convection from heated cylinder cases. Left Demirdžić case and right cooling of overhead line case.</caption>
 +
</figure>
 +
 +
 +
<figure id="fig:f12">
 +
[[File:TFC_temp.png|300px]][[File:TFC_vel.png|300px]]
 +
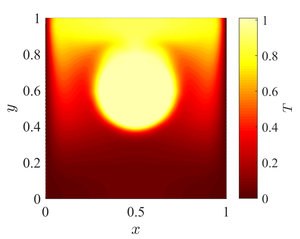
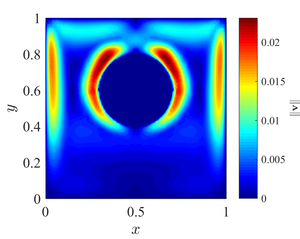
<caption>Temperature (left) and velocity maginute (right) contour plots for Demirdžić  case.</caption>
 +
</figure>
 +
 +
<figure id="fig:f12">
 +
[[File:TFC_demer_comp.png|300px]][[File:TFC_demer_Nu_comp.png|300px]]
 +
<caption>Comparison between MLSM solution and reference data in terms of isotherms (left) and cold side Nusselt number (right) for Demirdžić  case.</caption>
 +
</figure>
 +
 +
<figure id="fig:f12">
 +
[[File:solver_case_3_T.png|300px]][[File:solver_case_3_v.png|300px]]
 +
<caption>Temperature (left) and velocity maginute (right) contour plots for cooling of overhead power line.</caption>
 +
</figure>
 +
 +
<figure id="fig:f12">
 +
[[File:dtr.png|600px]]
 +
<caption>Power of convective cooling with respect to the difference between the skin temperature and ambiental temperature.</caption>
 
</figure>
 
</figure>
  

Latest revision as of 20:51, 22 October 2022

edit 

Related papers

M. Maksić, V. Djurica, A. Souvent, J. Slak, M. Depolli, G. Kosec; Cooling of overhead power lines due to the natural convection, International journal of electrical power & energy systems, 2019


Natural convection from a horizontal cylinder plays a crucial role in many heat transfer related problems ranging from heat exchangers, solar heating systems, cooling of electronic packages, to cooling of overhead power lines. One of the first studies of convective heat transfer from circular cylinders goes back to 1892 when Ayrton and Kilgour investigated the thermal emission of thin, long horizontal wires [1]. Several similar experiments followed [2], and in 1975 Morgan collected experimental data in a comprehensive review paper [3]. Based on the collected data Morgan introduced the correlations between Grashof, Prandtl and Nusselt numbers [3]. In other words, he presented relationships between the power of cooling in dependence on the material properties and the temperature difference between the cylinder and the ambient, which still serve as a basis in operative models for predicting the temperature of overhead power lines [4, 5]. There are many other similar studies where authors investigate the heat transfer from the heated cylinder due to the natural or forced convection under different conditions [2, 6, 7]. Benchmark case for the natural convection around the homogeneously heated cylinder was introduced in 1992 by Demirdžić, et al. [8]. The governing equations are the same as in De Vahl Davis natural convection test.

In Demirdžić case the natural convection from a cylinder whose wall is maintained at a constant temperature, enclosed by a square duct with vertical walls kept at constant temperature, and horizontal walls assumed adiabatic, is considered. The cylinder centre is displaced from the duct centre vertically for 10%, and its radius is 20% of domain height.

If we change boundary conditions in Demirdžić case we can also simulate cooling of overhead power line by natural convection. The problem is very similar to the previous one, with the main difference in a top boundary condition, where instead of confined cavity an open domain is assumed. Besides, the thermo-physical properties of real materials are considered and not dimensionless characterisation as in previous two examples. The power line 490-AL1/64-ST1A with radius 1.33 cm is positioned in the centre of in 5x5 cm square domain, and the air is modelled with following properties: $\rho =1.29\,\text{kg/}{{\text{m}}^{\text{3}}}$, ${{c}_{p}}=1005\,\text{J/kgK}$, $\beta=0.00367$, thermal conductivity modelled as ${{\lambda }_{a}}=2.368\cdot {{10}^{-2}}+7.23\cdot {{10}^{-5}}{{T}^{{}}}-2.763\cdot {{10}^{-8}}{{T}^{2}}\,\left[ \frac{\text{W}}{\text{mK}} \right]$ and viscosity modelled as $\mu =\left( 17.239+4.635\cdot {{10}^{-2}}T-2.03\cdot {{10}^{-5}}{{T}^{2}} \right)\cdot {{10}^{-6}}\left[ \text{Pa}\,\text{s} \right]$.

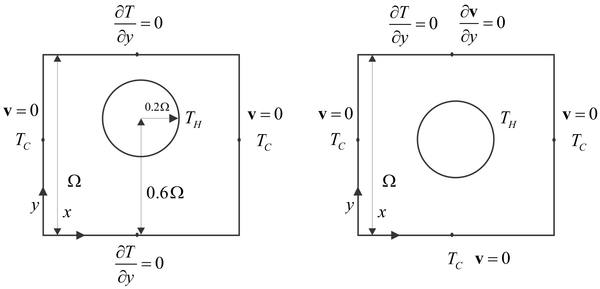Problem scheme.png Figure 1: Scheme of the natural convection from heated cylinder cases. Left Demirdžić case and right cooling of overhead line case.


TFC temp.pngTFC vel.png Figure 2: Temperature (left) and velocity maginute (right) contour plots for Demirdžić case.
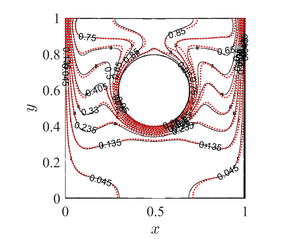
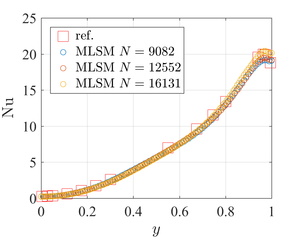TFC demer comp.pngTFC demer Nu comp.png Figure 3: Comparison between MLSM solution and reference data in terms of isotherms (left) and cold side Nusselt number (right) for Demirdžić case.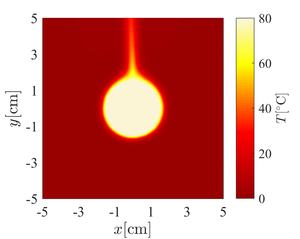
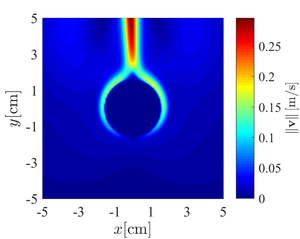Solver case 3 T.pngSolver case 3 v.png Figure 4: Temperature (left) and velocity maginute (right) contour plots for cooling of overhead power line.
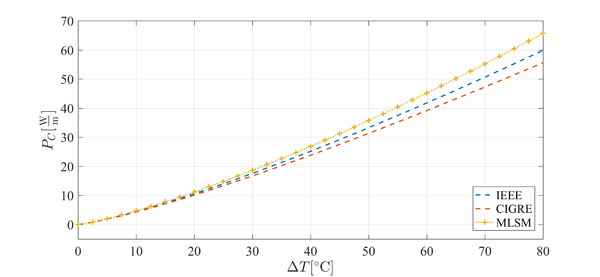Dtr.png Figure 5: Power of convective cooling with respect to the difference between the skin temperature and ambiental temperature.

[1] Ayrton, W. & Kilgour, H., The thermal emissivity of thin wires in air. . Philos TR Soc A, 183, pp. 371–405, 1892.

[2] Boetcher, S. K. S., Natural Convection from Circular Cylinders, Springer: Daytona Beach, 2014.

[3] Morgan, V., The overall convective heat transfer from smooth circular cylinders. Advances in Heat Transfer, 1, pp. 199-264, 1975.

[4] Guide for Thermal Rating Calculations of Overhead Lines. pp. 2014.

[5] IEEE Standard for Calculating the Current-Temperature Relationship of Bare Overhead Conductors. pp. 2014.

[6] Atmane, Mohamed A., Chan, Victor S.S. & Murray, Darina B., Natural convection around a horizontal heated cylinder: The effects of vertical confinement. International Journal of Heat and Mass Transfer, 46, pp. 3661-3672, 2003.

[7] Cesinia, G. , Paroncinia, M. , Cortellab G. & Manzanb, M., Natural convection from a horizontal cylinder in a rectangular cavity. International Journal of Heat and Mass Transfer, 42, pp. 1801-1811, 1999.

[8] Demirdžić, I., Lilek, Ž & Perić, M., Fluid flow and heat transfer test problems for non-orthogonal grids: Bench-mark solutions. International Journal for Numerical Methods in Fluids, 15, pp. 329–354, 1992.

Retrieved from "http://e6.ijs.si/medusa/wiki/index.php?title=Natural_convection_from_heated_cylinder&oldid=3456"