Difference between revisions of "De Vahl Davis natural convection test"
(→Results) |
E6WikiAdmin (talk | contribs) |
||
| (58 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | Click here to return back to [[Fluid Mechanics]] | ||
| + | |||
| + | {{Box-round|title= Related papers | | ||
| + | [https://e6.ijs.si/ParallelAndDistributedSystems/publications/992507.pdf G. Kosec, B. Šarler; Solution of thermo-fluid problems by collocation with local pressure correction, International journal of numerical methods for heat & fluid flow, vol.18, 2008] | ||
| + | |||
| + | [https://e6.ijs.si/ParallelAndDistributedSystems/publications/1905659.pdf G. Kosec, M. Založnik, B. Šarler, H. Combeau; A meshless approach towards solution of macrosegregation phenomena, Computers, materials & continua : CMC, vol. 22, 2011 ] | ||
| + | |||
| + | [http://comms.ijs.si/~gkosec/data/papers/27339815.pdf G. Kosec, M. Depolli, A. Rashkovska, R. Trobec; Super linear speedup in a local parallel meshless solution of thermo-fluid problem, Computers & Structures, vol. 133, 2014] | ||
| + | |||
| + | [https://e6.ijs.si/ParallelAndDistributedSystems/publications/3218939.pdf G. Kosec, B. Šarler; Simulation of macrosegregation with mesosegregates in binary metallic casts by a meshless method, Engineering analysis with boundary elements] | ||
| + | |||
| + | [https://e6.ijs.si/ParallelAndDistributedSystems/publications/32388135.pdf M. Maksić, V. Djurica, A. Souvent, J. Slak, M. Depolli, G. Kosec; Cooling of overhead power lines due to the natural convection, International journal of electrical power & energy systems, 2019] | ||
| + | }} | ||
| + | |||
=Intro= | =Intro= | ||
The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^5}$. Here we present a MLSM solution of the case. | The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^5}$. Here we present a MLSM solution of the case. | ||
| Line 23: | Line 37: | ||
=Code= | =Code= | ||
| − | + | Full examples can be found under the examples in the [https://gitlab.com/e62Lab/medusa code repository]. | |
| + | ==Explicit ACM method with CBS looks== | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
v2[boundary] = vec_t{0.0, 0.0}; | v2[boundary] = vec_t{0.0, 0.0}; | ||
| Line 61: | Line 76: | ||
for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0); | for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0); | ||
} | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | == Explicit pressure correction == | ||
| + | The solution of heat equation is the same as in above example | ||
| + | <syntaxhighlight lang="c++" line> | ||
| + | for (int step = 0; step <= O.t_steps; ++step) { | ||
| + | // Explicit Navier-Stokes computed on whole domain, including boundaries | ||
| + | // without pressure | ||
| + | for (int c:all) { | ||
| + | v_2[c] = v_1[c] + O.dt ( | ||
| + | O.mu / O.rho * op.lap(v_1, c) | ||
| + | - op.grad(v_1, c) * v_1[c] | ||
| + | + O.g * (1 - O.beta * (T_1[c] - O.T_ref))); | ||
| + | } | ||
| + | // Pressure correction | ||
| + | VecXd rhs_pressure(N + 1, 0); //Note N+1, +1 stands for regularization equation | ||
| + | rhs_pressure(N) = 0; // = 0 part of the regularization equation | ||
| + | for (int i:interior) rhs_pressure(c) = O.rho / O.dt * op.div(v_2, c); | ||
| + | for (int i: boundary) rhs_pressure(c) = O.rho / O.dt * v_2[c].dot(domain.normal(c)); | ||
| + | VecXd solution = solver_p.solve(rhs_pressure); | ||
| + | alpha = solution[N]; | ||
| + | VecXd P_c = solution.head(N); | ||
| + | for ( int i = interior) v_2[c] -= O.dt / O.rho * op.grad(P_c, c); | ||
| + | v_2[boundary] = 0; // force boundary conditions | ||
| + | //heat transport | ||
| + | for (auto c : interior) { | ||
| + | T2[c] = T1[c] + O.dt * O.lam / O.rho / O.c_p * op.lap(T1, c) - | ||
| + | O.dt * v1[c].transpose() * op.grad(T1, c); | ||
| + | } | ||
| + | for (auto c : top) T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0); | ||
| + | for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0); | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | == Implicit == | ||
| + | <syntaxhighlight lang="c++" line> | ||
| + | for (int step = 0; step <= O.t_steps_i; ++step) { | ||
| + | time_1 = std::chrono::high_resolution_clock::now(); | ||
| + | // NAVIER STOKES | ||
| + | M_velocity = mat_t(2 * N, 2 * N); | ||
| + | // system | ||
| + | M_velocity.reserve(Range<int>(2 * N, O.n)); | ||
| + | for (int i : interior) { | ||
| + | op.valuevec(M_velocity, i, 1 / O.dt_i); | ||
| + | op.lapvec(M_velocity, i, -O.mu / O.rho); | ||
| + | op.gradvec(M_velocity, i, v_1[i]); | ||
| + | } | ||
| + | for (int i : boundary) op.valuevec(M_velocity, i, 1); //sets velocity to 0 | ||
| + | |||
| + | M_velocity.makeCompressed(); | ||
| + | solver_v.compute(M_velocity); | ||
| + | // solution | ||
| + | Range <vec_t> rhs_vec(domain.size(), 0); | ||
| + | for (int i : interior) { | ||
| + | rhs_vec[i] = -1 / O.rho * op.grad(P, i) + | ||
| + | v_1[i] / O.dt_i | ||
| + | + O.g * (1 - O.beta * (T[i] - O.T_ref)); | ||
| + | } | ||
| + | // for (int i:top) rhs_vec[i] = vec_t{0,1}; | ||
| + | |||
| + | v_2 = reshape<2>(solver_v.solveWithGuess(reshape(rhs_vec), reshape(v_1))); | ||
| + | // END OF NAVIER STOKES | ||
| + | |||
| + | // PRESSURE CORRECTION | ||
| + | VecXd rhs_pressure(N + 1, 0); //Note N+1, +1 stands for regularization equation | ||
| + | rhs_pressure(N) = 0; // = 0 part of the regularization equation | ||
| + | double alpha; | ||
| + | for (int i : interior) rhs_pressure(i) = O.rho / O.dt_i * op.div(v_2, i); | ||
| + | for (int i : boundary) rhs_pressure(i) = O.rho / O.dt * v_2[i].dot(domain.normal(i)); | ||
| + | |||
| + | VecXd solution = solver_p.solve(rhs_pressure); | ||
| + | alpha = solution[N]; | ||
| + | VecXd P_c = solution.head(N); | ||
| + | // apply velocity correction | ||
| + | for (int i : interior) { | ||
| + | v_2[i] -= O.dl * O.dt_i / O.rho * op.grad(P_c, i); | ||
| + | } | ||
| + | P += O.dl * P_c; | ||
| + | // enforce velocity BC | ||
| + | // v_2[boundary] = 0; | ||
| + | // END OF PRESSURE CORRECTION | ||
| + | |||
| + | // HEAT TRANSPORT | ||
| + | M_temperature = mat_t(N, N); | ||
| + | Range<int> per_row(N, O.n); | ||
| + | M_temperature.reserve(per_row); | ||
| + | // outer boundary dirichlet BC | ||
| + | for (int i : top) op.neumann_implicit(M_temperature, i, domain.normal(i), 1); | ||
| + | for (int i : bottom) op.neumann_implicit(M_temperature, i, domain.normal(i), 1); | ||
| + | for (int i : left) op.value(M_temperature, i, 1.0); | ||
| + | for (int i : right) op.value(M_temperature, i, 1.0); | ||
| + | // heat transport in air | ||
| + | for (int i : interior) { | ||
| + | op.value(M_temperature, i, 1.0); // time dependency | ||
| + | op.lap(M_temperature, i, -O.dt_i * O.lam / O.rho / O.c_p); //laplace in interior | ||
| + | op.grad(M_temperature, i, O.dt * v_2[i]); | ||
| + | } | ||
| + | M_temperature.makeCompressed(); | ||
| + | solver_T.compute(M_temperature); | ||
| + | |||
| + | VectorXd rhs = VectorXd::Zero(N); | ||
| + | for (int i : interior) rhs(i) = T(i); | ||
| + | for (int i : top) rhs(i) = 0; | ||
| + | for (int i : bottom) rhs(i) = 0; | ||
| + | for (int i : left) rhs(i) = O.T_hot; | ||
| + | for (int i : right) rhs(i) = O.T_cold; | ||
| + | T = solver_T.solveWithGuess(rhs, T); | ||
| + | // END OF HEAT TRANSPORT | ||
| + | v_1.swap(v_2); | ||
| + | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
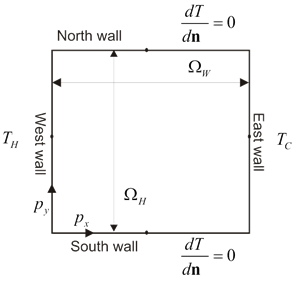
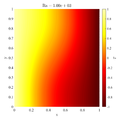
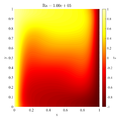
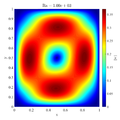
=Results= | =Results= | ||
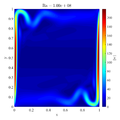
| − | + | == Comparison of MLSM solution with reference data == | |
| − | [[File:DeVahlDavisRa1e8.mp4]] | + | Following video shows evolution of temperature and velocity magnitude for the $Ra=10^8$ case. |
| − | + | ||
| + | [[File:DeVahlDavisRa1e8.mp4|640px]] | ||
| + | |||
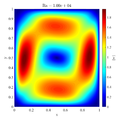
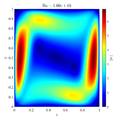
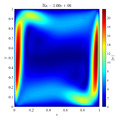
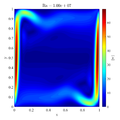
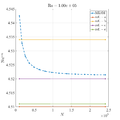
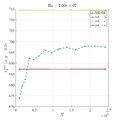
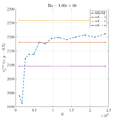
In below galley you can find temperature contour plots, velocity magnitude contour plots, v_max and average hot side Nusselt number convergence behavior. The reference values are from: | In below galley you can find temperature contour plots, velocity magnitude contour plots, v_max and average hot side Nusselt number convergence behavior. The reference values are from: | ||
Latest revision as of 20:54, 22 October 2022
Click here to return back to Fluid Mechanics
Related papers
Intro
The classical de Vahl Davis benchmark test is defined for the natural convection of the air ($\Pr =0.71$) in the square closed cavity (${{\text{A}}_{\text{R}}}=1$). The only physical free parameter of the test remains the thermal Rayleigh number. In the original paper [1] de Vahl Davis tested the problem up to the Rayleigh number ${{10}^{6}}$, however in the latter publications, the results of more intense simulations were presented with the Rayleigh number up to ${{10}^{8}}$. Lage and Bejan [2] showed that the laminar domain of the closed cavity natural convection problem is roughly below $\text{Gr1}{{\text{0}}^{9}}$. It was reported [3, 4] that the natural convection becomes unsteady for $\text{Ra}=2\cdot {{10}^5}$. Here we present a MLSM solution of the case.
\begin{equation} \text{Ra}\text{=}\,\frac{\left| \mathbf{g} \right|{{\beta }_{T}}\left( {{T}_{H}}-{{T}_{C}} \right){{\Omega }_{H}}^{3}{{\rho }^{2}}{{c}_{p}}}{\lambda \mu } \end{equation} \begin{equation} \text{Pr}=\frac{\mu {{c}_{p}}}{\lambda } \end{equation}
[1] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64.
[2] Lage JL, Bejan A. The Ra-Pr domain of laminar natural convection in an enclosure heated from the side. Numer Heat Transfer. 1991;A19:21-41.
[3] Janssen RJA, Henkes RAWM. Accuracy of finite-volume disretizations for the bifurcating natural-convection flow in a square cavity. Numer Heat Transfer. 1993;B24:191-207.
[4] Nobile E. Simulation of time-dependent flow in cavities with the additive-correction multigrid method, part II: Apllications. Numer Heat Transfer. 1996;B30:341-50.
Code
Full examples can be found under the examples in the code repository.
Explicit ACM method with CBS looks
1 v2[boundary] = vec_t{0.0, 0.0};
2 T2[left] = O.T_cold;
3 T2[right] = O.T_hot;
4 //Time stepping
5 for (int step = 0; step <= O.t_steps; ++step) {
6 for (int i_count = 1; i_count < _MAX_ITER_; ++i_count) {
7 // Navier Stokes
8 for (auto c : interior) {
9 v2[c] = v1[c] + O.dt * (-1 / O.rho * op.grad(P1, c)
10 + O.mu / O.rho * op.lap(v1, c)
11 - op.grad(v1, c) * v1[c]
12 + O.g * (1 - O.beta * (T1[c] - O.T_ref)));
13 }
14
15 //Speed of sound
16 Range<scal_t> norm = v2.map([](const vec_t& p) { return p.norm(); });
17 scal_t C = O.dl * std::max(*std::max_element(norm.begin(), norm.end()), O.v_ref);
18 // Mass continuity
19 Range<scal_t> div_v;
20 for (auto c:all) {
21 div_v[c] = op.div(v2, c);
22 P2[c] = P1[c] - C * C * O.dt * O.rho * div_v[c] +
23 O.dl2 * C * C * O.dt * O.dt * op.lap(P1, c);
24 }
25 P1.swap(P2);
26 }
27
28 //heat transport
29 for (auto c : interior) {
30 T2[c] = T1[c] + O.dt * O.lam / O.rho / O.c_p * op.lap(T1, c) -
31 O.dt * v1[c].transpose() * op.grad(T1, c);
32 }
33 for (auto c : top) T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0);
34 for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0);
35 }
Explicit pressure correction
The solution of heat equation is the same as in above example
1 for (int step = 0; step <= O.t_steps; ++step) {
2 // Explicit Navier-Stokes computed on whole domain, including boundaries
3 // without pressure
4 for (int c:all) {
5 v_2[c] = v_1[c] + O.dt (
6 O.mu / O.rho * op.lap(v_1, c)
7 - op.grad(v_1, c) * v_1[c]
8 + O.g * (1 - O.beta * (T_1[c] - O.T_ref)));
9 }
10 // Pressure correction
11 VecXd rhs_pressure(N + 1, 0); //Note N+1, +1 stands for regularization equation
12 rhs_pressure(N) = 0; // = 0 part of the regularization equation
13 for (int i:interior) rhs_pressure(c) = O.rho / O.dt * op.div(v_2, c);
14 for (int i: boundary) rhs_pressure(c) = O.rho / O.dt * v_2[c].dot(domain.normal(c));
15 VecXd solution = solver_p.solve(rhs_pressure);
16 alpha = solution[N];
17 VecXd P_c = solution.head(N);
18 for ( int i = interior) v_2[c] -= O.dt / O.rho * op.grad(P_c, c);
19 v_2[boundary] = 0; // force boundary conditions
20 //heat transport
21 for (auto c : interior) {
22 T2[c] = T1[c] + O.dt * O.lam / O.rho / O.c_p * op.lap(T1, c) -
23 O.dt * v1[c].transpose() * op.grad(T1, c);
24 }
25 for (auto c : top) T2[c] = op.neumann(T2, c, vec_t{0, -1}, 0.0);
26 for (auto c : bottom) T2[c] = op.neumann(T2, c, vec_t{0, 1}, 0.0);
27 }
Implicit
1 for (int step = 0; step <= O.t_steps_i; ++step) {
2 time_1 = std::chrono::high_resolution_clock::now();
3 // NAVIER STOKES
4 M_velocity = mat_t(2 * N, 2 * N);
5 // system
6 M_velocity.reserve(Range<int>(2 * N, O.n));
7 for (int i : interior) {
8 op.valuevec(M_velocity, i, 1 / O.dt_i);
9 op.lapvec(M_velocity, i, -O.mu / O.rho);
10 op.gradvec(M_velocity, i, v_1[i]);
11 }
12 for (int i : boundary) op.valuevec(M_velocity, i, 1); //sets velocity to 0
13
14 M_velocity.makeCompressed();
15 solver_v.compute(M_velocity);
16 // solution
17 Range <vec_t> rhs_vec(domain.size(), 0);
18 for (int i : interior) {
19 rhs_vec[i] = -1 / O.rho * op.grad(P, i) +
20 v_1[i] / O.dt_i
21 + O.g * (1 - O.beta * (T[i] - O.T_ref));
22 }
23 // for (int i:top) rhs_vec[i] = vec_t{0,1};
24
25 v_2 = reshape<2>(solver_v.solveWithGuess(reshape(rhs_vec), reshape(v_1)));
26 // END OF NAVIER STOKES
27
28 // PRESSURE CORRECTION
29 VecXd rhs_pressure(N + 1, 0); //Note N+1, +1 stands for regularization equation
30 rhs_pressure(N) = 0; // = 0 part of the regularization equation
31 double alpha;
32 for (int i : interior) rhs_pressure(i) = O.rho / O.dt_i * op.div(v_2, i);
33 for (int i : boundary) rhs_pressure(i) = O.rho / O.dt * v_2[i].dot(domain.normal(i));
34
35 VecXd solution = solver_p.solve(rhs_pressure);
36 alpha = solution[N];
37 VecXd P_c = solution.head(N);
38 // apply velocity correction
39 for (int i : interior) {
40 v_2[i] -= O.dl * O.dt_i / O.rho * op.grad(P_c, i);
41 }
42 P += O.dl * P_c;
43 // enforce velocity BC
44 // v_2[boundary] = 0;
45 // END OF PRESSURE CORRECTION
46
47 // HEAT TRANSPORT
48 M_temperature = mat_t(N, N);
49 Range<int> per_row(N, O.n);
50 M_temperature.reserve(per_row);
51 // outer boundary dirichlet BC
52 for (int i : top) op.neumann_implicit(M_temperature, i, domain.normal(i), 1);
53 for (int i : bottom) op.neumann_implicit(M_temperature, i, domain.normal(i), 1);
54 for (int i : left) op.value(M_temperature, i, 1.0);
55 for (int i : right) op.value(M_temperature, i, 1.0);
56 // heat transport in air
57 for (int i : interior) {
58 op.value(M_temperature, i, 1.0); // time dependency
59 op.lap(M_temperature, i, -O.dt_i * O.lam / O.rho / O.c_p); //laplace in interior
60 op.grad(M_temperature, i, O.dt * v_2[i]);
61 }
62 M_temperature.makeCompressed();
63 solver_T.compute(M_temperature);
64
65 VectorXd rhs = VectorXd::Zero(N);
66 for (int i : interior) rhs(i) = T(i);
67 for (int i : top) rhs(i) = 0;
68 for (int i : bottom) rhs(i) = 0;
69 for (int i : left) rhs(i) = O.T_hot;
70 for (int i : right) rhs(i) = O.T_cold;
71 T = solver_T.solveWithGuess(rhs, T);
72 // END OF HEAT TRANSPORT
73 v_1.swap(v_2);
74 }
Results
Comparison of MLSM solution with reference data
Following video shows evolution of temperature and velocity magnitude for the $Ra=10^8$ case.
In below galley you can find temperature contour plots, velocity magnitude contour plots, v_max and average hot side Nusselt number convergence behavior. The reference values are from:
- [a] de Vahl Davis G. Natural convection of air in a square cavity: a bench mark numerical solution. Int J Numer Meth Fl. 1983;3:249-64.
- [b] Sadat H, Couturier S. Performance and accuracy of a meshless method for laminar natural convection. Numer Heat Transfer. 2000;B37:455-67.
- [c] Wan DC, Patnaik BSV, Wei GW. A new benchmark quality solution for the buoyancy-driven cavity by discrete singular convolution. Numer Heat Transfer. 2001;B40:199-228.
- [d] Šarler B. A radial basis function collocation approach in computational fluid dynamics. CMES-Comp Model Eng. 2005;7:185-93.
- [e] Kosec G, Šarler B. Solution of thermo-fluid problems by collocation with local pressure correction. Int J Numer Method H. 2008;18:868-82.