Difference between revisions of "K-d tree"

From Medusa: Coordinate Free Mehless Method implementation
Jump to: navigation, search
m (Grammar)
 
(20 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 +
{{DISPLAYTITLE:''k''-d tree}}
 
In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space.  
 
In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space.  
−
In unstructured mesh based approaches, support domains can be determined from the mesh topology. However, in meshless methods, the nearest neighboring nodes in $\Omega_S$ are determined with various algorithms and specialized data structures, we use kD Tree.
+
In unstructured mesh based approaches, support domains can be determined from the mesh connectivity relations.  
 +
However, in meshless methods, the stencil/support nodes are usually chosen as the nearest $n$ visible nodes.  
  
−
The input to Algorithm is a list of $(n_S +1)$ nearest nodes to ${\bf x}$. A naive implementation of finding these nodes could become quite complex if implemented with classical sorting of all nodal distances. Regarding the number of nodes $N$, it approaches the quadratic computational complexity. However, by using efficient data structures, e.g. quadtree, R tree or kD tree (2D tree for 2D domains), the problem becomes tractable.  
+
In order to compute nearest neighbors effectively, fast spatial search structures have been developed, such as [https://en.wikipedia.org/wiki/Octree octree], [https://en.wikipedia.org/wiki/Ball_tree ball tree], [https://en.wikipedia.org/wiki/Cover_tree cover tree] and [https://en.wikipedia.org/wiki/K-d_tree $k$-d tree]. All of these structures first take a list of $N$ points and build a search structure, enabling  subsequent queries for $n$ nearest neighbors to be answered in $O(n\log N)$ time.
−
The strategy is to build the data structure only once, before the solution procedure. During the solution, the support nodes of the desired points will then be found much faster.
+
The $k$-d tree structure is described below to give the reader a basic idea of how such spatial structures store data.
  
 
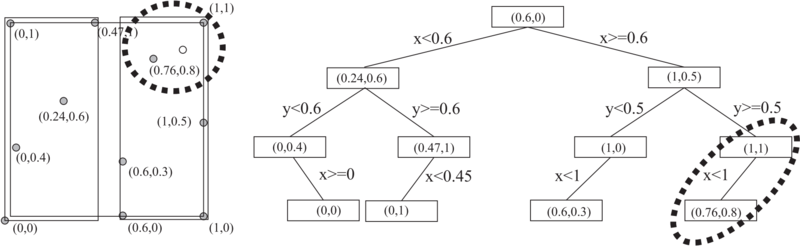
[[File:image_1avj3kcbe157a1ad610k81brmgsj9.png|800px|thumb|<caption> 2D tree example</caption>]]
 
[[File:image_1avj3kcbe157a1ad610k81brmgsj9.png|800px|thumb|<caption> 2D tree example</caption>]]
  
−
Kd tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the node in a tree. At depth $k$, the k-th axis (dimenison) is used to divide the remaining points. Example: in 3 dimensions we have x,y and z axes. At root level we decide to divide points according to their $x$ values (we could also do it according to y or z values). Usual criterion for divison of points is median. Thus, at root level, we look for median point by looking at x coordiantes of all points. We put the median point into the root leaf. Remaining points are put into the left and right subtrees. We put the points which have smaller x coorinate into the left subtree and points which have larger x coorinate into the right subtree (or vice versa). We construct the two children nodes of the root from the two subgroups we just created. The procedure is the same, except that we divide the space according to y or z coordinate. We continue this way until we run out of points. The axes used for median search are periodically repeating.
+
A $k$-d tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the node in a tree. At depth $k$, the $k$-th axis (dimenison) is used to divide the remaining points. Example: in 3 dimensions we have $x$, $y$ and $z$ axes. At root level we decide to divide points according to their $x$ values (we could also do it according to $y$ or $z$ values). Usual criterion for division of points is the median. Thus, at root level, we look for median point by looking at $x$ coordiantes of all points. We put the median point into the root leaf. Remaining points are put into the left and right subtrees. We put the points which have smaller $x$ coorinate into the left subtree and points which have larger $x$ coordinate into the right subtree (or vice versa). We construct the two children nodes of the root from the two subgroups we just created. The procedure is the same, except that we divide the space according to $y$ or $z$ coordinate. We continue this way until we run out of points. The axes used for median search are periodically repeating.
  
−
The procedure described above is used to construct a tree from a collection of given points and is used by ANN library. The tree can also be constructed by inserting points one by one. Such procedure is used by Libssrckdtree library. Time complexity of both procedures is $o(nlogn)$. The most time consuming part of the former algorithm is median point selection. It's time complexity is o(n). This can be improved by imploying some smarter schemes than median finding (consult literature). Time complexity of the second algorithm can quickly be calculated from the average time need to insert a node into the tree - it scales o($log n$). Inserting n nodes thus again results in $n log n$ time complexity.
+
Often, dynamic search structures are needed as well, which support node insertion and removal. In the beginning we were using [http://www.cs.umd.edu/~mount/ANN/ ANN] and [https://www.savarese.com/software/libssrckdtree/ libssrckdtree]
 +
libraries for static and dynamic spatial search structures, respectively. Later, we tested four different publicly available C++ libraries that support at least static spatial search:
  
−
We tested build times for Ann and Libssrckdtree libraries. We also included a cover tree library, which can be found [https://github.com/DNCrane/Cover-Tree here].
+
* [http://www.cs.umd.edu/~mount/ANN/ ANN]
 +
* [https://www.savarese.com/software/libssrckdtree/ libssrckdtree]
 +
* [http://spatial.sourceforge.net/ spatial]
 +
* [https://github.com/jlblancoc/nanoflann/ nanoflann]
  
−
[[File:Tree_building_time.jpg]]
+
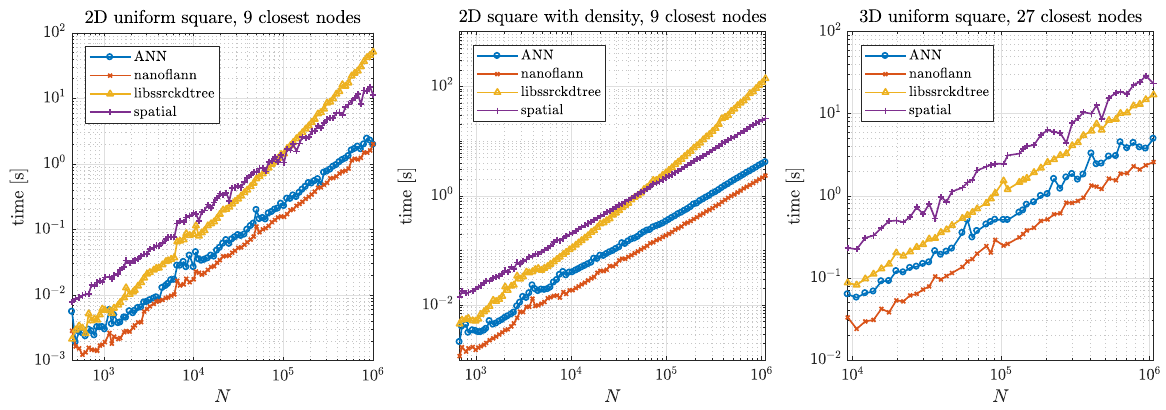
Two typical usage examples for these structures were tested. First, we tested a typical example of finding support domains of $n$ nodes for all nodes, which includes building a tree from a set of points and finding $n$ closest nodes for each point. The results are shown below.
  
−
Nearest neighbor search is a $log n$ procedure, although in practice, especially in higher dimensions, it's closer to o(n). There is a nice description of the algorithm on [https://en.wikipedia.org/wiki/K-d_tree wikipedia] website. We tested ANN and Libssrckdtree implementations. In addition we tested also cover tree nearest neighbor search.
+
[[File:kdtree_find_support_time.png]]
  
−
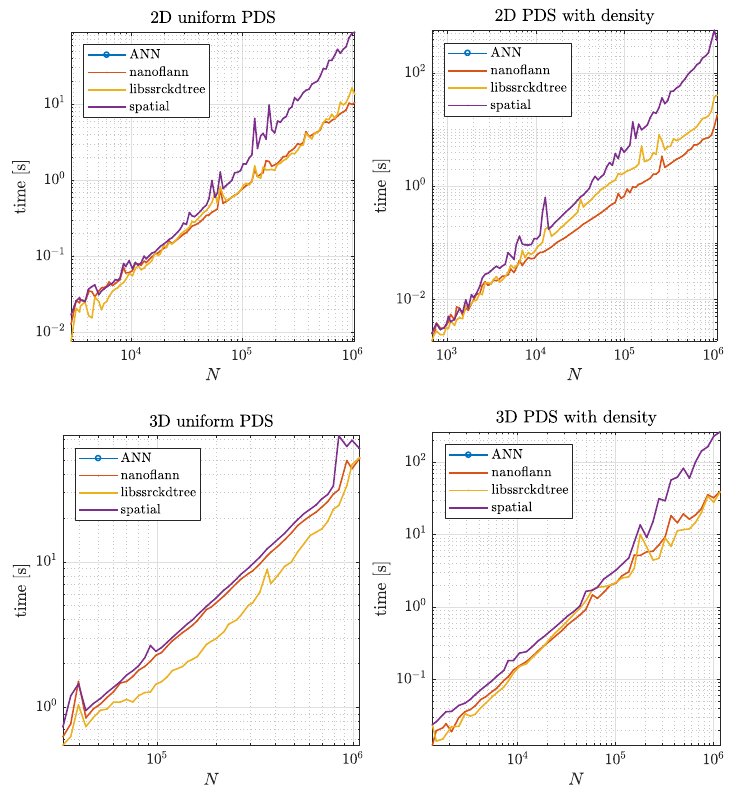
[[File:nearest_neighbor_search_time.jpg|800px]]
+
Second, we tested how the structures performed during the node generation process, as described in [[Positioning of computational nodes]] page. Results are shown in figure below.
 +
 
 +
[[File:kdtree_pds_time.png]]
 +
 
 +
Besides speed, which was the main factor, we also considered the number of dependencies a library has and how general it is regarding distances and data types.
 +
Overall, we decided to use the [https://github.com/jlblancoc/nanoflann/ nanoflann] library in [http://e6.ijs.si/medusa/ medusa]. Our wrappers are available
 +
as [http://e6.ijs.si/medusa/docs/html/classmm_1_1KDTree.html KDTree] and [http://e6.ijs.si/medusa/docs/html/classmm_1_1KDTreeMutable.html KDTreeMutable].
 +
 
 +
The results and reasoning is described more accurately in the technical report [[:File:report.pdf]].
  
−
Note that cover tree implementation is not the best available, but it is the only one to have insert/remove and is written in c++.
 
−
 
  
 
<!--
 
<!--
Line 56: Line 68:
  
 
== References ==
 
== References ==
−
* Trobec R., Kosec G., Šterk M., Šarler B., Comparison of local weak and strong form meshless methods for 2-D diffusion equation. Engineering analysis with boundary elements. 2012;36:310-321;
+
* Trobec R., Kosec G., Parallel scientific computing: theory, algorithms, and applications of mesh based and meshless methods: Springer; 2015.
−
* Trobec R., Kosec G., Parallel scientific computing : theory, algorithms, and applications of mesh based and meshless methods: Springer; 2015.
 
−
* k-d tree. (n.d.). In Wikipedia. Retrieved March 17, 2017, from https://en.wikipedia.org/wiki/K-d_tree
 

Latest revision as of 13:30, 16 June 2022

In structured meshes, neighborhood relations are implicitly determined by the mapping from the physical to the logical space. In unstructured mesh based approaches, support domains can be determined from the mesh connectivity relations. However, in meshless methods, the stencil/support nodes are usually chosen as the nearest $n$ visible nodes.

In order to compute nearest neighbors effectively, fast spatial search structures have been developed, such as octree, ball tree, cover tree and $k$-d tree. All of these structures first take a list of $N$ points and build a search structure, enabling subsequent queries for $n$ nearest neighbors to be answered in $O(n\log N)$ time. The $k$-d tree structure is described below to give the reader a basic idea of how such spatial structures store data.

2D tree example

A $k$-d tree is a binary tree which uses hyperplane space partitioning to divide points into subgroups (subtrees). The plane is chosen based on the depth of the node in a tree. At depth $k$, the $k$-th axis (dimenison) is used to divide the remaining points. Example: in 3 dimensions we have $x$, $y$ and $z$ axes. At root level we decide to divide points according to their $x$ values (we could also do it according to $y$ or $z$ values). Usual criterion for division of points is the median. Thus, at root level, we look for median point by looking at $x$ coordiantes of all points. We put the median point into the root leaf. Remaining points are put into the left and right subtrees. We put the points which have smaller $x$ coorinate into the left subtree and points which have larger $x$ coordinate into the right subtree (or vice versa). We construct the two children nodes of the root from the two subgroups we just created. The procedure is the same, except that we divide the space according to $y$ or $z$ coordinate. We continue this way until we run out of points. The axes used for median search are periodically repeating.

Often, dynamic search structures are needed as well, which support node insertion and removal. In the beginning we were using ANN and libssrckdtree libraries for static and dynamic spatial search structures, respectively. Later, we tested four different publicly available C++ libraries that support at least static spatial search:

Two typical usage examples for these structures were tested. First, we tested a typical example of finding support domains of $n$ nodes for all nodes, which includes building a tree from a set of points and finding $n$ closest nodes for each point. The results are shown below.

Kdtree find support time.png

Second, we tested how the structures performed during the node generation process, as described in Positioning of computational nodes page. Results are shown in figure below.

Kdtree pds time.png

Besides speed, which was the main factor, we also considered the number of dependencies a library has and how general it is regarding distances and data types. Overall, we decided to use the nanoflann library in medusa. Our wrappers are available as KDTree and KDTreeMutable.

The results and reasoning is described more accurately in the technical report File:report.pdf.


References

  • Trobec R., Kosec G., Parallel scientific computing: theory, algorithms, and applications of mesh based and meshless methods: Springer; 2015.
Retrieved from "http://e6.ijs.si/medusa/wiki/index.php?title=K-d_tree&oldid=3192"