Difference between revisions of "1D MLSM and FDM comparison"
(→Neumann case) |
(→Neumann case) |
||
| Line 27: | Line 27: | ||
* symmetric finite difference <math>f'(0) \approx (f_1 - f_{-1}) / h</math> and normal discretization in node 0 <math>f'(0) \approx (f_1 - 2f_0 + f_-1) /h^23</math> | * symmetric finite difference <math>f'(0) \approx (f_1 - f_{-1}) / h</math> and normal discretization in node 0 <math>f'(0) \approx (f_1 - 2f_0 + f_-1) /h^23</math> | ||
* onsided double finite difference <math>f'(0) \approx (-3/2 f_0 + 2f_1 - -1/2 f_2) / h</math> | * onsided double finite difference <math>f'(0) \approx (-3/2 f_0 + 2f_1 - -1/2 f_2) / h</math> | ||
| + | |||
| + | MLSM with support size $n = 3$ and three polynomial basis functions results in exactly the FDM method with onesided double finite difference approximation. | ||
| + | |||
| + | [[File:neucmp.png|800px]][[File:neutimecmp.png|800px]] | ||
Revision as of 10:57, 13 March 2017
Different numerical approaches to solving a Dirichlet or Neumann problem
\(
\begin{align*}
\text{Dirichlet} && \text{Neumann} \\
f''(x) &= 2x^2+5 \text{ on } (0, 1) & f''(x) &= 2x^2+5 \text{ on } (0, 1) \\
f(0) &= 1 & f'(0) &= 1 \\
f(1) &= 1 & f(1) &= 1 \\
f(x) &= \frac{1}{6} \left(x^4+15 x^2-16 x+6\right) & f(x) &= \frac{1}{6} \left(x^4+15 x^2+6 x-16\right)
\end{align*}
\)
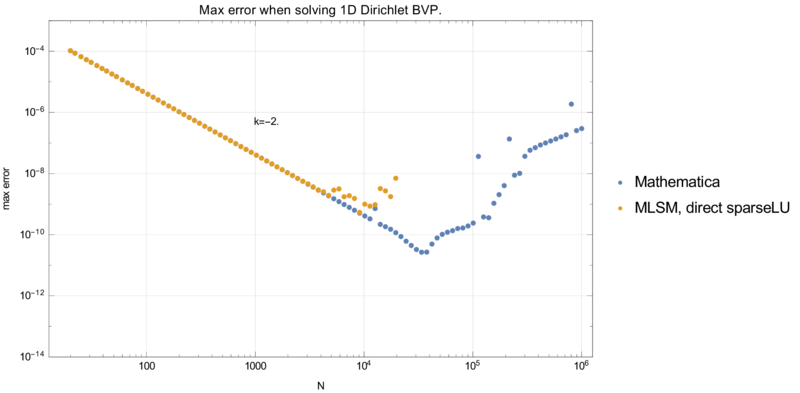
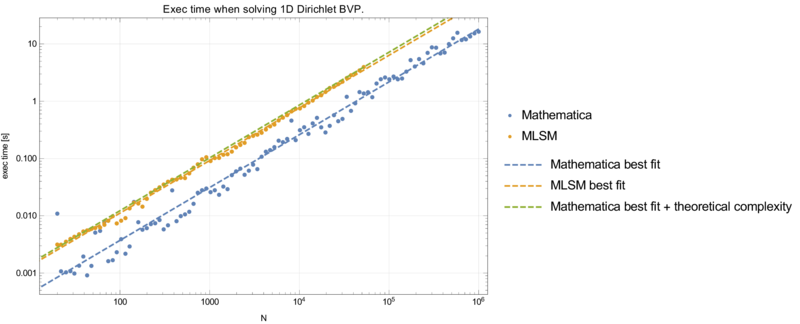
were analysed. Theoretically, FDM and MLSM should match completely. This is practivaly demonstrated up to certain discretization level.
The interval \([0, 1]\) was always discretized uniformly using $N$ nodes, \(x_i = a+i h, h = (b-a)/N\).
Dirichlet case
Precision and execution time are summarised in graphs below.
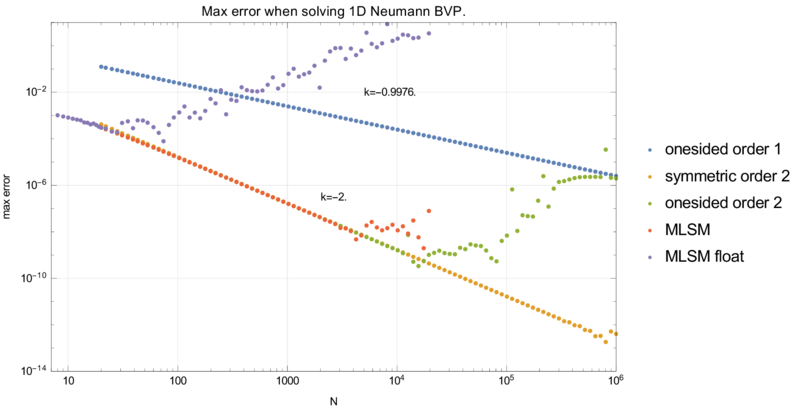
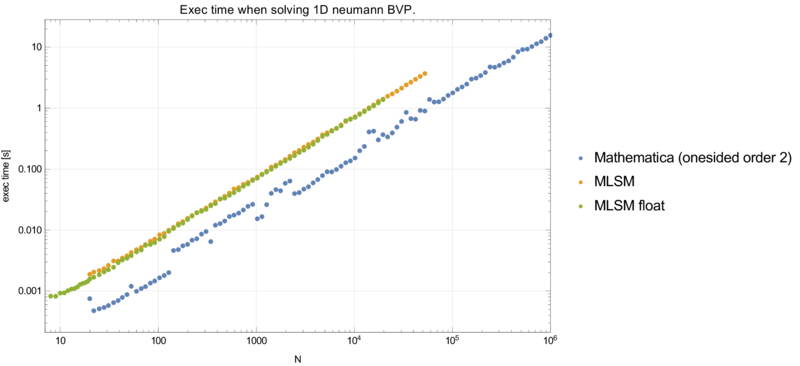
Neumann case
We have more that one possible disctretization of the Neumann BC in point 0. Three explored options are:
- onsided finite difference \(f'(0) \approx (f_1 - f_0) / h\)
- symmetric finite difference \(f'(0) \approx (f_1 - f_{-1}) / h\) and normal discretization in node 0 \(f'(0) \approx (f_1 - 2f_0 + f_-1) /h^23\)
- onsided double finite difference \(f'(0) \approx (-3/2 f_0 + 2f_1 - -1/2 f_2) / h\)
MLSM with support size $n = 3$ and three polynomial basis functions results in exactly the FDM method with onesided double finite difference approximation.