Difference between revisions of "1D MLSM and FDM comparison"
(→Dirichlet case) |
(→Neumann case) |
||
| Line 24: | Line 24: | ||
Three explored options are: | Three explored options are: | ||
| − | + | * onsided finite difference <math>f'(0) \approx (f_1 - f_0) / h</math> | |
| − | + | * symmetric finite difference <math>f'(0) \approx (f_1 - f_{-1}) / h</math> and normal discretization in node 0 <math>f'(0) \approx (f_1 - 2f_0 + f_-1) /h^23</math> | |
| − | + | * onsided double finite difference <math>f'(0) \approx (-3/2 f_0 + 2f_1 - -1/2 f_2) / h</math> | |
Revision as of 10:52, 13 March 2017
Different numerical approaches to solving a Dirichlet or Neumann problem
\(
\begin{align*}
\text{Dirichlet} && \text{Neumann} \\
f''(x) &= 2x^2+5 \text{ on } (0, 1) & f''(x) &= 2x^2+5 \text{ on } (0, 1) \\
f(0) &= 1 & f'(0) &= 1 \\
f(1) &= 1 & f(1) &= 1 \\
f(x) &= \frac{1}{6} \left(x^4+15 x^2-16 x+6\right) & f(x) &= \frac{1}{6} \left(x^4+15 x^2+6 x-16\right)
\end{align*}
\)
were analysed. Theoretically, FDM and MLSM should match completely. This is practivaly demonstrated up to certain discretization level.
The interval \([0, 1]\) was always discretized uniformly using $N$ nodes, \(x_i = a+i h, h = (b-a)/N\).
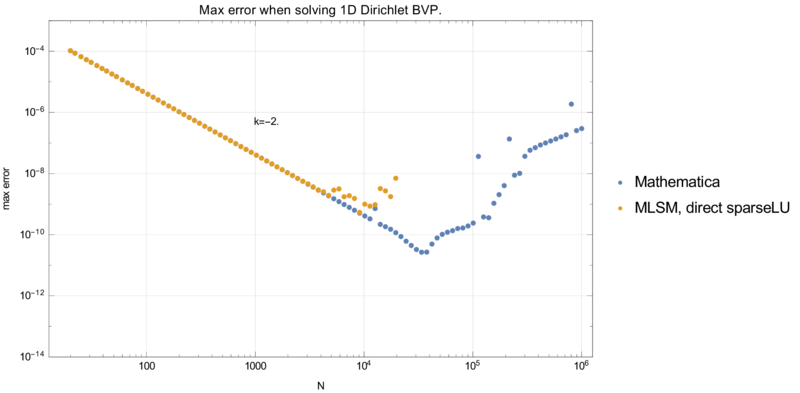
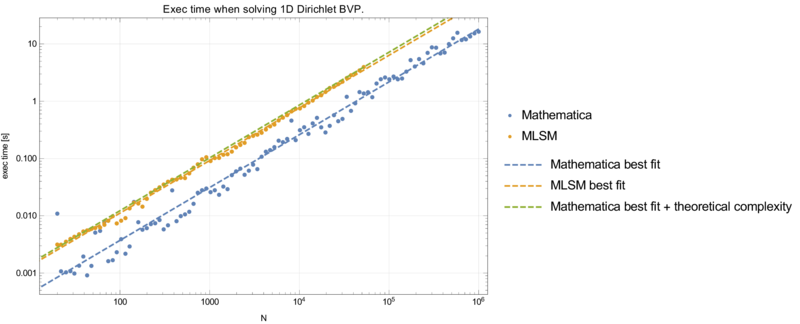
Dirichlet case
Precision and execution time are summarised in graphs below.
Neumann case
We have more that one possible disctretization of the Neumann BC in point 0. Three explored options are:
- onsided finite difference \(f'(0) \approx (f_1 - f_0) / h\)
- symmetric finite difference \(f'(0) \approx (f_1 - f_{-1}) / h\) and normal discretization in node 0 \(f'(0) \approx (f_1 - 2f_0 + f_-1) /h^23\)
- onsided double finite difference \(f'(0) \approx (-3/2 f_0 + 2f_1 - -1/2 f_2) / h\)