Difference between revisions of "Cantilever beam"
(→Numerical solution) |
|||
| Line 97: | Line 97: | ||
[[File:cantilever_beam.png|800px]] | [[File:cantilever_beam.png|800px]] | ||
| + | ==Reference test== | ||
| + | This is the text that you are going to verify with a reference.<ref>Reference details go here</ref> | ||
| + | |||
| + | ==References== | ||
| + | {{Reflist}} | ||
Revision as of 10:28, 15 November 2016
Do you want to go back to Solid Mechanics?
On this page we conduct numerical studies of bending of a cantilever loaded at the end, a common numerical benchmark in elastostatics.
Contents
Exact solution
The exact solutions to this problem is given in Timoshenko (1951) where it derived for plane stress conditions. Consider a beam of dimensions $L \times D$ having a narrow rectangular cross section. The origin of the coordinate system is placed at $(x,y) = (0,D/2)$. The beam is bent by a force $P$ applied at the end $x = 0$ and the other end of the beam is fixed (at $x = L$). The stresses in such a beam are given as: \begin{equation} \sigma_{xx} = -\frac{Pxy}{I}, \end{equation} \begin{equation} \sigma_{yy} = 0, \end{equation} \begin{equation}\label{eq:sxy} \sigma_{xy} = -\frac{P}{2I}\left(\left(\frac{D}{2}\right)^2 - y^2 \right), \end{equation} where $I = D^3/12$ is the moment of inertia.
The exact solution in terms of the displacements in $x$- and $y-$ direction is \begin{align}\label{eq:beam_a1} u_x(x,y) &= -\frac{Py}{6EI}\left(3(x^2-L^2) -(2+\nu)y^2 + 6 (1+\nu) \frac{D^2}{4}\right) \\ \label{eq:beam_a2} u_y(x,y) &= \frac{P}{6EI}\left(3\nu x y^2 + x^3 - 3L^2 x + 2L^3\right) \end{align} where $E$ is Young's modulus and $\nu$ is the Poisson ratio.
Numerical solution
For the numerical solution we first choose the following parameters:
- Loading: $P = -1000$ N
- Young's modulus: $E = 3 \times 10^7$ N/m2
- Poisson's ratio: $\nu = 0.3$
- Height of the beam: $D = 12$ m
- Length of the beam: $L = 48$ m
The unloaded beam is discretized with $40 \times 10$ regular nodes. Since the right end of the beam at $x = L$ is fixed, the displacement boundary conditions are prescribed from the known analytical formulae (\ref{eq:beam_a1}) and (\ref{eq:beam_a2}) : \begin{equation} u_x(L,y) = -\frac{P}{6EI}\left(-(2+\nu)y^2 + 6 (1+\nu) \frac{D^2}{4}\right); \qquad u_y(L,y) = \frac{P}{2EI}(\nu L y^2) \end{equation} The traction boundary at the left end of the beam ($x=0$) is given by (\ref{eq:sxy}): \begin{equation}\label{eq:trac_a} t_y(L,y) = -\frac{P}{2I}\left(\left(\frac{D}{2}\right)^2 - y^2 \right). \end{equation}
An indicator of the accuracy that can be employed is the strain energy error $e$: \begin{equation} e = \left[ \frac{1}{2} \int_\Omega (\b{\varepsilon}^\mathrm{num} - \b{\varepsilon}^\mathrm{exact})\b{C}(\b{\varepsilon}^\mathrm{num} - \b{\varepsilon}^\mathrm{exact}) d\Omega\right]^{1/2} \end{equation} where $\b{\varepsilon}$ is the strain tensor in vector form, $\b{C}$ the reduced stiffness tensor (a matrix) and $\Omega$ the domain of the calculated solution.
FreeFem++
The required code to solve this problem in FreeFem++ is
// Parameters real E = 3.0e7, nu = 0.3; real P = -1000; real L = 48, D = 12; real I = D^3/12; // Mesh mesh Th = square(40,10,[L*x,-D/2+D*y]); // Macros macro u [ux,uy] // displacement macro v [vx,vy] // test function macro div(u) (dx(u[0])+dy(u[1])) // divergence macro eM(u) [dx(u[0]), dy(u[1]), sqrt(2)*(dx(u[1]) + dy(u[0]))/2] // strain tensor // Finite element space fespace Vh(Th,[P2,P2]); Vh u, v; // Boundary conditions func uxb = -P*y/(6*E*I)*(nu*y^2-2*(1+nu)*y^2+6*D^2/4*(1+nu)); func uyb = P/(6*E*I)*(3*nu*L*y^2); func ty = -P/(2*I)*(D^2/4-y^2); // Convert E and nu to plane stress E = E/(1-nu^2); nu = nu/(1-nu); // Lame parameters real mu = E/(2*(1+nu)); real lambda = E*nu/((1+nu)*(1-2*nu)); // Solve problem solve cantileverBeam(u,v) = int2d(Th)(lambda*div(u)*div(v) + 2*mu*(eM(u)'*eM(v))) - int1d(Th,4)([0,-ty]'*v) + on(2,ux=uxb,uy=uyb); // Plot solution real coef = 1000; Th = movemesh(Th,[x+ux*coef,y+uy*coef]); plot(Th,wait=1);
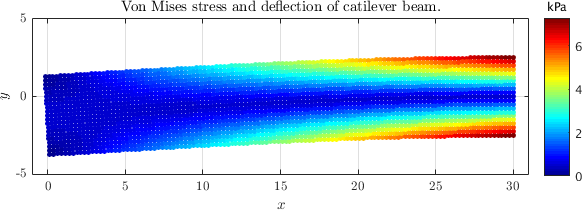
The numerical solutions for beam displacements $u_y(x,0)$ in the axial direction of the beam, and shear stresses $\sigma_{xy}(L/2,y)$ in a cross section at the half lengthwise of the beam, obtained by quadratic finite elements are shown in the figure below. Analytic solutions are shown with continuous lines.
Reference test
This is the text that you are going to verify with a reference.[1]
References
End notes
- ↑ Reference details go here