Difference between revisions of "Burgers' equation"
m (Added link to repository) |
|||
| (9 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
\end{equation} | \end{equation} | ||
| − | where $\b{u}$ is a velocity field. | + | where $\b{u}$ is a velocity vector field and $\nu$ is the dynamic viscosity. To solve the equation we will linearize the advection term. There are several tactics of linearization, but we choose the simplest one, which is using the previous velocity as an approximation of the current velociy. Using the implicit Euler method we arrive at the equation |
\begin{equation} | \begin{equation} | ||
| Line 19: | Line 19: | ||
\end{equation} | \end{equation} | ||
| − | This will be rewritten into a linear system of equations with Medusa and then solved with Eigen. Let's look at the code(find the full version | + | This will be rewritten into a linear system of equations with Medusa and then solved with Eigen. Let's look at the code (find the full version on our [https://gitlab.com/e62Lab/medusa/-/tree/dev/examples?ref_type=heads repository]). First we construct our 1D domain with length 2l, discretize it with a given step dx and find the closest $n$ nodes of each node which are called stencil nodes or support nodes or simply the stencil. |
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| Line 27: | Line 27: | ||
int domain_size = discretization.size(); | int domain_size = discretization.size(); | ||
// Find support nodes | // Find support nodes | ||
| − | FindClosest find_support( | + | FindClosest find_support(n); |
discretization.findSupport(find_support); | discretization.findSupport(find_support); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | + | We will use the RBF-FD method with polyharmonic splines of order 3 as Radial Basis Functions (RBFs) augmented with monomials up to 4th order for our approximation engine. We use it in conjunction with stencil nodes to compute the stencil weights (also called shape functions) which are used in approximations of differential operators on our domain. | |
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
Polyharmonic<double, 3> p; | Polyharmonic<double, 3> p; | ||
Monomials<Vec1d> mon(4); | Monomials<Vec1d> mon(4); | ||
| − | RBFFD<Polyharmonic<double, 3>, Vec1d, ScaleToClosest> | + | RBFFD<Polyharmonic<double, 3>, Vec1d, ScaleToClosest> approx(p, mon); |
| − | |||
auto storage = discretization.computeShapes(approx); | auto storage = discretization.computeShapes(approx); | ||
| − | VectorXd | + | |
| + | VectorXd u = VectorXd::Zero(domain_size); // vector for containing the current state | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | + | Next we set the initial condition to | |
| + | |||
| + | \begin{equation} | ||
| + | u(x) = \frac{2\nu ak\sin(kx)}{b + a\cos(kx)}, | ||
| + | \end{equation} | ||
| + | where $a, b, k$ are constants and $\nu$ is viscosity. We chose this function because it has an analytical solution<ref name="Burgers' equation">A. Salih, Burgers' equation. Indian Institute of Space Science and Technology, Thiruvananthapuram, 2016.</ref> | ||
| + | |||
| + | \begin{equation} | ||
| + | u(x, t) = \frac{2\nu ake^{-\nu k^2t}\sin(kx)}{b + ae^{-\nu k^2t}\cos(kx)}, | ||
| + | \end{equation} | ||
| + | |||
| + | which we will compare our solution to. It is derived using the Cole-Hopf transformation of a solution of the diffusion equation with the initial profile: $f(x) = b + a\cos(kx)$ for $b>a$. | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
//Set initial condition | //Set initial condition | ||
for (int i : discretization.all()){ | for (int i : discretization.all()){ | ||
| − | + | u(i) = 2*nu*a*k*std::sin(k*discretization.pos(i,0))/(b+a*std::cos(k*discretization.pos(i,0))); | |
| − | |||
</syntaxhighlight> | </syntaxhighlight> | ||
| Line 54: | Line 64: | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
for (tt = 1; tt <= t_steps; ++tt) { | for (tt = 1; tt <= t_steps; ++tt) { | ||
| − | SparseMatrix<double> M(domain_size, domain_size); | + | SparseMatrix<double> M(domain_size, domain_size); |
VectorXd rhs = VectorXd::Zero(domain_size); | VectorXd rhs = VectorXd::Zero(domain_size); | ||
M.reserve(Range<int>(domain_size, n)); | M.reserve(Range<int>(domain_size, n)); | ||
| − | auto op = storage.implicitOperators(M, rhs); | + | auto op = storage.implicitOperators(M, rhs); |
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Now comes the crucial part - setting the equation. In essence, we rewrite equation (3) in Medusa's terms. Terms on the left hand side are written into matrix $M$ and the terms on the right into $rhs$. The terms with the prefix op. are matrices that represent the | + | Now comes the crucial part - setting the equation. In essence, we rewrite equation (3) in Medusa's terms. Terms on the left hand side are written into matrix $M$ and the terms on the right into $rhs$. The terms with the prefix op. are matrices that represent the appropriate differential operators (op.value(i) is a matrix with $A_{ii}$ = 1 and zero everywhere else), vector u[i] represents $\b{u}_i^{n-1}$ - result of the previous step. |
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| − | // Setting the equation | + | // Setting the equation interior |
for (int i : interior) { | for (int i : interior) { | ||
| − | op.value(i) + ( | + | op.value(i) + (u[i] * dt) * op.der1(i, 0) + (-dt*nu) * op.der2(i, 0, 0) = u[i]; |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Boundary conditions are handled in the same way. | + | Boundary conditions are handled in the same way. The analytical solution is defined on an infinite domain, but we see from equation (5) that $u = 0$ for $kx = z\pi, z \in \mathbb{Z}$. So we will be able to enforce Dirichlet boundary conditions on a finite domain, but this will limit our choice of $k$ to $\frac{z\pi}{l}, z \in \mathbb{Z}$, where $l$ is the length of the domain. |
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
// Setting Dirichlet boundary conditions | // Setting Dirichlet boundary conditions | ||
| Line 77: | Line 87: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | We then solve the equation and update | + | We then solve the equation and update u for use in the next time step. The solution is also saved into an output file with HDF5. |
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| − | M.makeCompressed(); | + | M.makeCompressed(); |
| − | BiCGSTAB<SparseMatrix<double, RowMajor>> solver; | + | BiCGSTAB<SparseMatrix<double, RowMajor>> solver; |
| − | solver.compute(M); | + | solver.compute(M); |
// Solve the linear system and update the state | // Solve the linear system and update the state | ||
| − | VectorXd | + | VectorXd u2 = solver.solve(rhs); |
| − | + | u = u2; | |
if (tt%(t_factor) == 0) { | if (tt%(t_factor) == 0) { | ||
| Line 96: | Line 106: | ||
hdf_out.writeDoubleAttribute("time",(t_0 + tt * dt)); | hdf_out.writeDoubleAttribute("time",(t_0 + tt * dt)); | ||
++t_save; | ++t_save; | ||
| − | hdf_out.writeDoubleArray(" | + | hdf_out.writeDoubleArray("u", u); |
| − | + | } | |
</syntaxhighlight> | </syntaxhighlight> | ||
=Results in 1D= | =Results in 1D= | ||
| − | For | + | For the simulation bellow we used the following parameters: $\nu = 0.05, l = 1, a = 4, b = 4.1, k = 2\pi$, $n = 13$, $m = 4$, $dx = 2\cdot 10^{-3}$, $dt = 10^{-6}$. |
| − | |||
| − | \nu | ||
| − | l | ||
| − | a | ||
| − | b | ||
| − | k | ||
| − | |||
| − | n | ||
| − | m | ||
| − | \ | ||
| − | |||
| − | [[File:Burgers_animation.mp4|400px]] | + | [[File:Burgers_animation.mp4|400px|center]] |
| − | =Convergence= | + | ==Convergence== |
<b>Spatial discretization</b> | <b>Spatial discretization</b> | ||
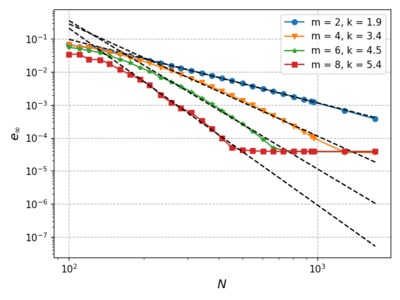
| − | We | + | We fix the time step to $dt = 10^{-6}$, vary the monomial augmentation order $m \in \{2, 4, 6, 8\}$ and analyze the convergence with increasing number of discretization nodes $N$. |
| − | After some initial | + | After some initial oscillation the maximum error decreases approximately as $\left(\frac{1}{N}\right)^k$, which is proportional to $dx^k$, where $k$ is the fit parameter for the function: $\log_{10}e_\infty = -k\log_{10}N + c$ for every $m$. But eventually the error plateaus because for finer spatial discretizations we are bounded by the time step. |
| − | [[File:Error_step6.png|400px]] | + | [[File:Error_step6.png|400px|center]] |
<b>Temporal discretization</b> | <b>Temporal discretization</b> | ||
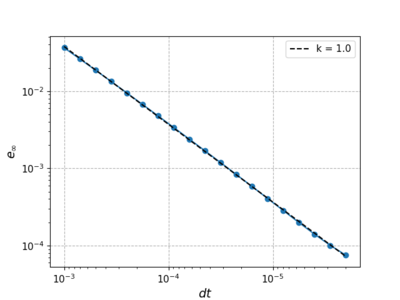
| − | Now we fix $N$ and $m$ to 1024 and 4 and vary the size of the time step from $10^{-3}$ to $10^{-6}$. The error decreases linearly with the time step. | + | Now we fix $N$ and $m$ to 1024 and 4 respectively and vary the size of the time step from $10^{-3}$ to $10^{-6}$. The error decreases linearly with the time step. |
| − | [[File: | + | [[File:Burgers1D_time_err.png|400px|center]] |
=Solution in 2D= | =Solution in 2D= | ||
| Line 137: | Line 136: | ||
\frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = \nu\nabla^2v, | \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = \nu\nabla^2v, | ||
\end{gather} | \end{gather} | ||
| − | where $u$ and $v$ are | + | |
| + | where $u$ and $v$ are velocities in the $x$ and $y$ direction respectively. We discretize equations (4) and (5) in the same way as in the 1D case: | ||
\begin{gather} | \begin{gather} | ||
u^{n}_i + \Bigl[u^{n-1}_i\frac{\partial u^{n}}{\partial x} + v^{n-1}_i\frac{\partial u^{n}}{\partial y} - \nu\nabla^2u^{n}\Bigr]\Delta t = u^{n-1}_i ,\\ | u^{n}_i + \Bigl[u^{n-1}_i\frac{\partial u^{n}}{\partial x} + v^{n-1}_i\frac{\partial u^{n}}{\partial y} - \nu\nabla^2u^{n}\Bigr]\Delta t = u^{n-1}_i ,\\ | ||
v^{n}_i + \Bigl[u^{n-1}_i\frac{\partial v^{n}}{\partial x} + v^{n-1}_i\frac{\partial v^{n}}{\partial y} - \nu\nabla^2v^{n}\Bigr]\Delta t = v^{n-1}_i . | v^{n}_i + \Bigl[u^{n-1}_i\frac{\partial v^{n}}{\partial x} + v^{n-1}_i\frac{\partial v^{n}}{\partial y} - \nu\nabla^2v^{n}\Bigr]\Delta t = v^{n-1}_i . | ||
\end{gather} | \end{gather} | ||
| − | We will solve each equation separately every time step, this will enable us to partialy parallelize the algorithm. First we contruct a 2D square domain with side length of 1 and find | + | |
| + | Find the full version of the code in our repository. We will solve each equation separately every time step, this will enable us to partialy parallelize the algorithm. First we contruct a 2D square domain with side length of 1, fill it with nodes and find 45 closest nodes of each node. | ||
| + | |||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
| − | BoxShape<Vec2d> b((0, 0), ( | + | BoxShape<Vec2d> b((0, 0), (1, 1)); |
| − | double step = | + | double step = 0.05; |
| − | auto discretization = b.discretizeBoundaryWithStep( | + | auto discretization = b.discretizeBoundaryWithStep(dr); |
GeneralFill<Vec2d> fill; fill.seed(0); | GeneralFill<Vec2d> fill; fill.seed(0); | ||
discretization.fill(fill, step); | discretization.fill(fill, step); | ||
| − | // Find support nodes | + | // Find support nodes, excluding boundary nodes from supports of boundary nodes for better stability of neumann BC |
| − | discretization.findSupport(FindClosest(n)); | + | discretization.findSupport(FindClosest(n).forNodes(discretization.interior())); |
| + | discretization.findSupport(FindClosest(n).forNodes(discretization.boundary()).searchAmong(discretization.interior()).forceSelf(true)); | ||
int domain_size = discretization.size(); | int domain_size = discretization.size(); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | We will be simulating the following initial and boundary conditions: | + | |
| + | The approximation engine is created and shape functions are computed in the same way as in the 1D example, except the template parameter is <code>Vec2d</code> instead of <code>Vec1d</code>. We will be simulating the following initial and boundary conditions: | ||
| + | |||
\begin{gather*} | \begin{gather*} | ||
u(x,y,0) = sin(\pi x)cos(\pi y),\\ | u(x,y,0) = sin(\pi x)cos(\pi y),\\ | ||
v(x,y,0) = cos(\pi x)sin(\pi y),\\ | v(x,y,0) = cos(\pi x)sin(\pi y),\\ | ||
| − | u(0,y,t)=u(1,y,t)=v(x,0,t)=v(x,1,t)=0. | + | u(0,y,t)=u(1,y,t)=v(x,0,t)=v(x,1,t)=0,\\ |
| + | \frac{\partial u}{\partial y}\bigg|_{y = 0} = \frac{\partial u}{\partial y}\bigg|_{y = 1} = \frac{\partial v}{\partial x}\bigg|_{x = 0} = \frac{\partial v}{\partial x}\bigg|_{x = 1} = 0. | ||
\end{gather*} | \end{gather*} | ||
| − | The analytical solution is given here <ref name="Analytical 2D">Q. Gao, M.Y. Zou, An analytical solution for two and three dimensional nonlinear Burgers' equation, Applied Mathematical Modelling, Volume 45, 2017, Pages 255-270, ISSN 0307-904X, https://doi.org/10.1016/j.apm.2016.12.018.</ref>. In the time stepping loop we use <code>#pragma omp parallel sections</code> to enable concurrent solving for $u$ and $v$. In each section we define separate | + | |
| + | The analytical solution is given here <ref name="Analytical 2D">Q. Gao, M.Y. Zou, An analytical solution for two and three dimensional nonlinear Burgers' equation, Applied Mathematical Modelling, Volume 45, 2017, Pages 255-270, ISSN 0307-904X, https://doi.org/10.1016/j.apm.2016.12.018.</ref>. In the time stepping loop we use <code>#pragma omp parallel sections</code> to enable concurrent solving for $u$ and $v$. In each section we define separate matrices Mu or Mv, rhs vectors rhu and rhv, and implicit operators opu and opv which will write into their respective matrices. The code bellow includes only the section for $u$. The types -1 ,-2 , -3 ,-4 correspond to the left, right, bottom and top boundaries. At the end of each section the velocities are updated. | ||
<syntaxhighlight lang="c++" line> | <syntaxhighlight lang="c++" line> | ||
for (tt = 1; tt <= t_steps; ++tt) { | for (tt = 1; tt <= t_steps; ++tt) { | ||
| − | double t = | + | double t = tt * dt; |
#pragma omp parallel sections shared(domain_size, discretization, storage, dt, u, v) | #pragma omp parallel sections shared(domain_size, discretization, storage, dt, u, v) | ||
| Line 170: | Line 177: | ||
#pragma omp section | #pragma omp section | ||
{ | { | ||
| − | SparseMatrix<double, RowMajor> Mu(domain_size, domain_size); | + | SparseMatrix<double, RowMajor> Mu(domain_size, domain_size); |
| − | VectorXd rhu = VectorXd::Zero(domain_size); | + | VectorXd rhu = VectorXd::Zero(domain_size); |
auto opu = storage.implicitOperators(Mu, rhu); | auto opu = storage.implicitOperators(Mu, rhu); | ||
Mu.reserve(storage.supportSizes()); | Mu.reserve(storage.supportSizes()); | ||
| Line 193: | Line 200: | ||
opu.value(i) = 0.0; | opu.value(i) = 0.0; | ||
} | } | ||
| + | |||
Mu.makeCompressed(); | Mu.makeCompressed(); | ||
BiCGSTAB<SparseMatrix<double, RowMajor>> solveru; // Creating solver object | BiCGSTAB<SparseMatrix<double, RowMajor>> solveru; // Creating solver object | ||
solveru.compute(Mu); // Initialize the iterative solver | solveru.compute(Mu); // Initialize the iterative solver | ||
VectorXd u2 = solveru.solve(rhu); | VectorXd u2 = solveru.solve(rhu); | ||
| − | u = u2; | + | u = u2; // update velocity vector |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
=Results in 2D= | =Results in 2D= | ||
| − | For | + | We use the RBF-FD method with PHS radial basis function $\phi(r) = r^3$ augmented with monomials. For the simulation bellow we used parameters $\nu = 1$, $n$ = 45, $m = 4$, $dr = 0.02$, $dt = 10^{-5}$. The animations below show the velocities in both directions and the magnitude of the velocity. |
| + | |||
[[File:Burgers2D_u.mp4|360px]] [[File:Burgers2D_v.mp4|360px]] [[File:Burgers2D_norm.mp4|360px]] | [[File:Burgers2D_u.mp4|360px]] [[File:Burgers2D_v.mp4|360px]] [[File:Burgers2D_norm.mp4|360px]] | ||
| + | ==Convergence== | ||
| + | <b>Spatial discretization</b> | ||
| + | |||
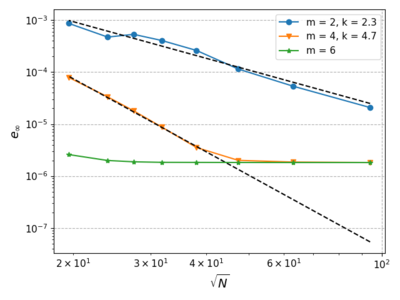
| + | We fix the time step to $dt = 10^{-6}$ and change the augmentation monomial order. The rate at which the maximum error decreases is close to $\left(\frac{1}{\sqrt{N}}\right)^{k}$ as shown on the graph bellow. The distance between neighbouring nodes in 2D is approximately proportional to $\frac{1}{\sqrt{N}}$ if the node distribution is uniform. For finer discretizations and bigger $m$ the error becomes approximately constant as we are again bounded by the time step. | ||
| + | |||
| + | [[File:Burgers2D_error_step.png|400px||center]] | ||
| + | |||
| + | <b>Temporal discretization</b> | ||
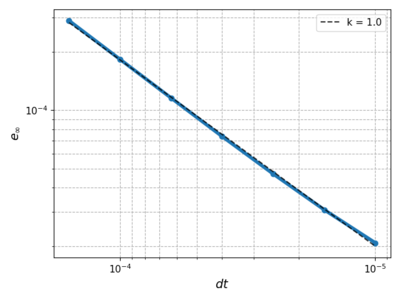
| + | We fix $m = 4$, $dr = 0.02$ giving us $N = 753$ and vary the time step size. The error decreases linearily as in the 1D case. | ||
| + | [[File:Burgers2D_time_error.png|400px||center]] | ||
=References= | =References= | ||
Latest revision as of 17:11, 26 August 2024
Let us consider the Burgers' equation, which describes the dynamics of viscous fluid without the effects of pressure. Despite being unrealistic, it is the simplest description of advective flow with diffusive effects of viscosity. It has the following form: \begin{equation} \frac{\partial \b{u}}{\partial t} + (\b{u}\cdot\nabla)\b{u} = \nu \nabla^2 \b{u} , \end{equation}
where $\b{u}$ is a velocity vector field and $\nu$ is the dynamic viscosity. To solve the equation we will linearize the advection term. There are several tactics of linearization, but we choose the simplest one, which is using the previous velocity as an approximation of the current velociy. Using the implicit Euler method we arrive at the equation
\begin{equation} \b{u}^{n}_i + \Bigl[\b{u}^{n-1}_i\cdot\nabla_i\b{u}^{n} - \nu\nabla^2_i \b{u}^{n}\Bigr]\Delta t = \b{u}^{n-1}_i, \end{equation}
where the subscript $i$ is the index of the domain node, superscripts $n$ and $n-1$ denote the current and the previous time step respectively, $\Delta t$ is the length of the time step. The notation $\nabla_i$ means the gradient operator at node $i$, not the component of the gradient. Same holds for $\nabla^2_i$. Using the Medusa library, this equation can be solved for $\b{u}^{n}_i$.
Contents
Solution in 1D
Let's look at an example in 1D with Dirichlet boundary conditions. We are solving the equivalent of equation (2) but with only one spatial variable: \begin{equation} u^{n}_i + \Bigl[u^{n-1}_i\frac{\partial u^{n}}{\partial x} - \nu\frac{\partial^2 u^{n}}{\partial x^2}\Bigr]\Delta t = u^{n-1}_i ,\\ u_i = 0 \text{ on } \partial \Omega . \end{equation}
This will be rewritten into a linear system of equations with Medusa and then solved with Eigen. Let's look at the code (find the full version on our repository). First we construct our 1D domain with length 2l, discretize it with a given step dx and find the closest $n$ nodes of each node which are called stencil nodes or support nodes or simply the stencil.
1 // Build 1D domain
2 BoxShape<Vec1d> domain((-l), (l)); // the interval [-l, l]
3 auto discretization = domain.discretizeWithStep(dx);
4 int domain_size = discretization.size();
5 // Find support nodes
6 FindClosest find_support(n);
7 discretization.findSupport(find_support);
We will use the RBF-FD method with polyharmonic splines of order 3 as Radial Basis Functions (RBFs) augmented with monomials up to 4th order for our approximation engine. We use it in conjunction with stencil nodes to compute the stencil weights (also called shape functions) which are used in approximations of differential operators on our domain.
1 Polyharmonic<double, 3> p;
2 Monomials<Vec1d> mon(4);
3 RBFFD<Polyharmonic<double, 3>, Vec1d, ScaleToClosest> approx(p, mon);
4 auto storage = discretization.computeShapes(approx);
5
6 VectorXd u = VectorXd::Zero(domain_size); // vector for containing the current state
Next we set the initial condition to
\begin{equation} u(x) = \frac{2\nu ak\sin(kx)}{b + a\cos(kx)}, \end{equation} where $a, b, k$ are constants and $\nu$ is viscosity. We chose this function because it has an analytical solution[1]
\begin{equation} u(x, t) = \frac{2\nu ake^{-\nu k^2t}\sin(kx)}{b + ae^{-\nu k^2t}\cos(kx)}, \end{equation}
which we will compare our solution to. It is derived using the Cole-Hopf transformation of a solution of the diffusion equation with the initial profile: $f(x) = b + a\cos(kx)$ for $b>a$.
1 //Set initial condition
2 for (int i : discretization.all()){
3 u(i) = 2*nu*a*k*std::sin(k*discretization.pos(i,0))/(b+a*std::cos(k*discretization.pos(i,0)));
Inside our time-stepping loop, we instantiate the matrix $M$ and the vector $rhs$ representing the linear system. We then construct the differential operators for implicit solving.
1 for (tt = 1; tt <= t_steps; ++tt) {
2 SparseMatrix<double> M(domain_size, domain_size);
3 VectorXd rhs = VectorXd::Zero(domain_size);
4 M.reserve(Range<int>(domain_size, n));
5 auto op = storage.implicitOperators(M, rhs);
Now comes the crucial part - setting the equation. In essence, we rewrite equation (3) in Medusa's terms. Terms on the left hand side are written into matrix $M$ and the terms on the right into $rhs$. The terms with the prefix op. are matrices that represent the appropriate differential operators (op.value(i) is a matrix with $A_{ii}$ = 1 and zero everywhere else), vector u[i] represents $\b{u}_i^{n-1}$ - result of the previous step.
1 // Setting the equation interior
2 for (int i : interior) {
3 op.value(i) + (u[i] * dt) * op.der1(i, 0) + (-dt*nu) * op.der2(i, 0, 0) = u[i];
4 }
Boundary conditions are handled in the same way. The analytical solution is defined on an infinite domain, but we see from equation (5) that $u = 0$ for $kx = z\pi, z \in \mathbb{Z}$. So we will be able to enforce Dirichlet boundary conditions on a finite domain, but this will limit our choice of $k$ to $\frac{z\pi}{l}, z \in \mathbb{Z}$, where $l$ is the length of the domain.
1 // Setting Dirichlet boundary conditions
2 for (int i : boundary) {
3 op.value(i) = 0;
4 }
We then solve the equation and update u for use in the next time step. The solution is also saved into an output file with HDF5.
1 M.makeCompressed();
2 BiCGSTAB<SparseMatrix<double, RowMajor>> solver;
3 solver.compute(M);
4
5 // Solve the linear system and update the state
6 VectorXd u2 = solver.solve(rhs);
7 u = u2;
8
9 if (tt%(t_factor) == 0) {
10 // Saving state in output file
11 hdf_out.openGroup("/step" + std::to_string(t_save));
12 hdf_out.writeSparseMatrix("M", M);
13 hdf_out.writeDoubleAttribute("TimeStep", t_save);
14 std::cout<< "Time step " << t_save << " of " << t_steps/t_factor << "." << std::endl;
15 hdf_out.writeDoubleAttribute("time",(t_0 + tt * dt));
16 ++t_save;
17 hdf_out.writeDoubleArray("u", u);
18 }
Results in 1D
For the simulation bellow we used the following parameters: $\nu = 0.05, l = 1, a = 4, b = 4.1, k = 2\pi$, $n = 13$, $m = 4$, $dx = 2\cdot 10^{-3}$, $dt = 10^{-6}$.
Convergence
Spatial discretization
We fix the time step to $dt = 10^{-6}$, vary the monomial augmentation order $m \in \{2, 4, 6, 8\}$ and analyze the convergence with increasing number of discretization nodes $N$.
After some initial oscillation the maximum error decreases approximately as $\left(\frac{1}{N}\right)^k$, which is proportional to $dx^k$, where $k$ is the fit parameter for the function: $\log_{10}e_\infty = -k\log_{10}N + c$ for every $m$. But eventually the error plateaus because for finer spatial discretizations we are bounded by the time step.
Temporal discretization
Now we fix $N$ and $m$ to 1024 and 4 respectively and vary the size of the time step from $10^{-3}$ to $10^{-6}$. The error decreases linearly with the time step.
Solution in 2D
In 2D the Burgers' equation (1) gives a system of two coupled nonlinear equations: \begin{gather} \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \nu\nabla^2u,\\ \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = \nu\nabla^2v, \end{gather}
where $u$ and $v$ are velocities in the $x$ and $y$ direction respectively. We discretize equations (4) and (5) in the same way as in the 1D case: \begin{gather} u^{n}_i + \Bigl[u^{n-1}_i\frac{\partial u^{n}}{\partial x} + v^{n-1}_i\frac{\partial u^{n}}{\partial y} - \nu\nabla^2u^{n}\Bigr]\Delta t = u^{n-1}_i ,\\ v^{n}_i + \Bigl[u^{n-1}_i\frac{\partial v^{n}}{\partial x} + v^{n-1}_i\frac{\partial v^{n}}{\partial y} - \nu\nabla^2v^{n}\Bigr]\Delta t = v^{n-1}_i . \end{gather}
Find the full version of the code in our repository. We will solve each equation separately every time step, this will enable us to partialy parallelize the algorithm. First we contruct a 2D square domain with side length of 1, fill it with nodes and find 45 closest nodes of each node.
1 BoxShape<Vec2d> b((0, 0), (1, 1));
2 double step = 0.05;
3 auto discretization = b.discretizeBoundaryWithStep(dr);
4 GeneralFill<Vec2d> fill; fill.seed(0);
5 discretization.fill(fill, step);
6 // Find support nodes, excluding boundary nodes from supports of boundary nodes for better stability of neumann BC
7 discretization.findSupport(FindClosest(n).forNodes(discretization.interior()));
8 discretization.findSupport(FindClosest(n).forNodes(discretization.boundary()).searchAmong(discretization.interior()).forceSelf(true));
9 int domain_size = discretization.size();
The approximation engine is created and shape functions are computed in the same way as in the 1D example, except the template parameter is Vec2d instead of Vec1d. We will be simulating the following initial and boundary conditions:
\begin{gather*} u(x,y,0) = sin(\pi x)cos(\pi y),\\ v(x,y,0) = cos(\pi x)sin(\pi y),\\ u(0,y,t)=u(1,y,t)=v(x,0,t)=v(x,1,t)=0,\\ \frac{\partial u}{\partial y}\bigg|_{y = 0} = \frac{\partial u}{\partial y}\bigg|_{y = 1} = \frac{\partial v}{\partial x}\bigg|_{x = 0} = \frac{\partial v}{\partial x}\bigg|_{x = 1} = 0. \end{gather*}
The analytical solution is given here [2]. In the time stepping loop we use #pragma omp parallel sections to enable concurrent solving for $u$ and $v$. In each section we define separate matrices Mu or Mv, rhs vectors rhu and rhv, and implicit operators opu and opv which will write into their respective matrices. The code bellow includes only the section for $u$. The types -1 ,-2 , -3 ,-4 correspond to the left, right, bottom and top boundaries. At the end of each section the velocities are updated.
1 for (tt = 1; tt <= t_steps; ++tt) {
2
3 double t = tt * dt;
4
5 #pragma omp parallel sections shared(domain_size, discretization, storage, dt, u, v)
6 {
7 ////Solving for u////
8 #pragma omp section
9 {
10 SparseMatrix<double, RowMajor> Mu(domain_size, domain_size);
11 VectorXd rhu = VectorXd::Zero(domain_size);
12 auto opu = storage.implicitOperators(Mu, rhu);
13 Mu.reserve(storage.supportSizes());
14
15 // Setting the equation
16 #pragma omp parallel for
17 for (int i : discretization.interior()) {
18 opu.value(i) + (u[i]*dt) * opu.der1(i, 0) + (v[i]*dt) * opu.der1(i, 1) + (-1/rndls*dt) * opu.lap(i) = u[i];
19 }
20 // Boundary conditions
21 for (int i : discretization.types() == -3){
22 opu.value(i) = analytical_u(discretization.pos(i,0), discretization.pos(i,1), t, 1.0/rndls);
23 }
24 for (int i : discretization.types() == -4){
25 opu.value(i) = analytical_u(discretization.pos(i,0), discretization.pos(i,1), t, 1.0/rndls);
26 }
27 for (int i : discretization.types() == -1){
28 opu.value(i) = 0.0;
29 }
30 for (int i : discretization.types() == -2){
31 opu.value(i) = 0.0;
32 }
33
34 Mu.makeCompressed();
35 BiCGSTAB<SparseMatrix<double, RowMajor>> solveru; // Creating solver object
36 solveru.compute(Mu); // Initialize the iterative solver
37 VectorXd u2 = solveru.solve(rhu);
38 u = u2; // update velocity vector
39 }
Results in 2D
We use the RBF-FD method with PHS radial basis function $\phi(r) = r^3$ augmented with monomials. For the simulation bellow we used parameters $\nu = 1$, $n$ = 45, $m = 4$, $dr = 0.02$, $dt = 10^{-5}$. The animations below show the velocities in both directions and the magnitude of the velocity.
Convergence
Spatial discretization
We fix the time step to $dt = 10^{-6}$ and change the augmentation monomial order. The rate at which the maximum error decreases is close to $\left(\frac{1}{\sqrt{N}}\right)^{k}$ as shown on the graph bellow. The distance between neighbouring nodes in 2D is approximately proportional to $\frac{1}{\sqrt{N}}$ if the node distribution is uniform. For finer discretizations and bigger $m$ the error becomes approximately constant as we are again bounded by the time step.
Temporal discretization
We fix $m = 4$, $dr = 0.02$ giving us $N = 753$ and vary the time step size. The error decreases linearily as in the 1D case.
References
- ↑ A. Salih, Burgers' equation. Indian Institute of Space Science and Technology, Thiruvananthapuram, 2016.
- ↑ Q. Gao, M.Y. Zou, An analytical solution for two and three dimensional nonlinear Burgers' equation, Applied Mathematical Modelling, Volume 45, 2017, Pages 255-270, ISSN 0307-904X, https://doi.org/10.1016/j.apm.2016.12.018.