Difference between revisions of "Fluid Mechanics"
(→Explicit/Implicit pressure calculation) |
(→Numerical examples) |
||
| (95 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
= Introduction = | = Introduction = | ||
| − | Computational fluid dynamics (CFD) is a field of a great interest among researchers in many fields of science, e.g. studying mathematical fundaments of numerical methods, developing novel physical models, improving computer implementations, and many others. Pushing the limits of all | + | Computational fluid dynamics (CFD) is a field of a great interest among researchers in many fields of science, e.g. studying mathematical fundaments of numerical methods, developing novel physical models, improving computer implementations, and many others. Pushing the limits of all involved fields of science helps community to deepen the understanding of several natural and technological phenomena. Weather forecast, ocean dynamics, water transport, casting, various energetic studies, etc., are just few examples where fluid dynamics plays a crucial role. The core problem of the CFD is solving the Navier-Stokes Equation or its variants, e.g. Darcy or Brinkman equation for flow in porous media. Here, we discuss basic algorithms for solving CFD problems. Check reference list on the [[Medusa|main page]] for more details about related work. |
Long story short, we want to solve | Long story short, we want to solve | ||
\begin{equation} | \begin{equation} | ||
| − | \frac{\partial \b{v}}{\partial t}+ | + | \frac{\partial \b{v}}{\partial t}+\nabla \cdot ( \rho \b{vv}) = -\nabla p+ \nabla(\mu \nabla\b{v})+\b{f} |
\label{NavierStokes} | \label{NavierStokes} | ||
\end{equation} | \end{equation} | ||
| − | also known as a Navier-Stokes equation. | + | also known as a Navier-Stokes equation. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Note that the $\b{v}\b{v}$ stands for the tensor or dyadic product \[ \b{v}\b{v} = \b{v}\otimes\b{v} = \b{v}\b{v}^\T = \left[ \begin{matrix} | Note that the $\b{v}\b{v}$ stands for the tensor or dyadic product \[ \b{v}\b{v} = \b{v}\otimes\b{v} = \b{v}\b{v}^\T = \left[ \begin{matrix} | ||
| Line 21: | Line 14: | ||
{{v}_{n}}{{v}_{1}} & \cdots & {{v}_{n}}{{v}_{n}} \\ | {{v}_{n}}{{v}_{1}} & \cdots & {{v}_{n}}{{v}_{n}} \\ | ||
\end{matrix} \right]\] | \end{matrix} \right]\] | ||
| − | An example | + | |
| + | Combining equation \ref{NavierStokes} and mass contiunity equation | ||
| + | \begin{equation} | ||
| + | \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho {\bf{u}}) = 0. | ||
| + | \end{equation} | ||
| + | |||
| + | simplifies advection term into (see [https://en.wikipedia.org/wiki/Derivation_of_the_Navier%E2%80%93Stokes_equations] for derivation) | ||
| + | |||
| + | \[\frac{\partial \left( \rho \b{v} \right)}{\partial t}+\nabla \cdot \left( \rho \b{vv} \right)=\frac{\partial \left( \rho \b{v} \right)}{\partial t}+(\rho \b{v}\cdot \nabla )\cdot \b{v}. \] | ||
| + | |||
| + | An example of advection term in 2D would therefore be | ||
\[\left( \b{v}\cdot \nabla \right)\b{v}=\left( \left( \begin{matrix} | \[\left( \b{v}\cdot \nabla \right)\b{v}=\left( \left( \begin{matrix} | ||
u \\ | u \\ | ||
| Line 36: | Line 39: | ||
\end{matrix} \right)\] | \end{matrix} \right)\] | ||
| − | The goal of CFD is to solve system \ref{NavierStokes} and \ref{contuinity}. It is obvious that a special treatment will be needed to couple both equations. In following discussion we cover some basic approaches, how this can be accomplished. | + | |
| + | In many cases we are interested in the incompressible fluids (Ma<0.3), reducing the continuity equation to | ||
| + | \begin{equation} | ||
| + | \nabla \cdot \b{v}=0 | ||
| + | \label{contuinity} | ||
| + | \end{equation} | ||
| + | |||
| + | |||
| + | The goal of CFD is to solve system \ref{NavierStokes} and \ref{contuinity}. It is obvious that a special treatment will be needed to couple both equations. In the following discussion we cover some basic approaches, how this can be accomplished. | ||
= Solutions algorithms = | = Solutions algorithms = | ||
== Artificial compressibility method == | == Artificial compressibility method == | ||
The simplest, completely explicit approach, is an artificial compressibility method (ACM), where a compressibility term is included in the mass continuity | The simplest, completely explicit approach, is an artificial compressibility method (ACM), where a compressibility term is included in the mass continuity | ||
| − | \[\frac{\partial \b{v}}{\partial t}+(\b{v}\cdot\nabla )\b{v}=-\frac{1}{\rho }\nabla p+\ | + | \[\frac{\partial \b{v}}{\partial t}+(\b{v}\cdot\nabla )\b{v}=-\frac{1}{\rho }\nabla p+\nu {{\nabla }^{2}}\b{v}+\b{f}\] |
| − | \[\frac{\partial \rho }{\partial t}+\nabla \cdot \b{v}=0\] | + | \[\frac{ 1 }{ \rho } \frac{\partial \rho }{\partial t}+\nabla \cdot \b{v}=0\] |
| − | \[\frac{\partial \rho }{\partial p}\frac{\partial p}{\partial t}+\nabla \cdot \b{v}=0\] | + | \[\frac{ 1 }{ \rho } \frac{\partial \rho }{\partial p}\frac{\partial p}{\partial t}+\nabla \cdot \b{v}=0\] |
Now, the above system can be solved directly. | Now, the above system can be solved directly. | ||
| Line 55: | Line 66: | ||
$C$ [m/s] - speed of sound | $C$ [m/s] - speed of sound | ||
\[\frac{1}{C^2}=\frac{\partial \rho }{\partial p}\] | \[\frac{1}{C^2}=\frac{\partial \rho }{\partial p}\] | ||
| − | Or in | + | Or in other words |
\[C^2=\left( \frac{\partial p}{\partial \rho}\right)_S\] | \[C^2=\left( \frac{\partial p}{\partial \rho}\right)_S\] | ||
where $\rho$ is the density of the material. It follows, by replacing partial derivatives, that the isentropic compressibility can be expressed as: | where $\rho$ is the density of the material. It follows, by replacing partial derivatives, that the isentropic compressibility can be expressed as: | ||
| Line 67: | Line 78: | ||
the same time must be as small as possible to minimizing perturbations on the incompressibility | the same time must be as small as possible to minimizing perturbations on the incompressibility | ||
equation. Therefore, $C$ influences the convergence rate and stability of the solution method. In other words, | equation. Therefore, $C$ influences the convergence rate and stability of the solution method. In other words, | ||
| − | assists in reducing large disparity in the eigenvalues, leading to a well-conditioned system. Values | + | assists in reducing large disparity in the eigenvalues, leading to a well-conditioned system. |
| − | + | The $C$ can be '''estimated''' with | |
| + | |||
| + | \[ C = \beta \max \left( \left|\b{v}\right|_2, \left|\b{v}_{ref}\right|_2 \right),\] | ||
| + | where $\b{v}_{ref}$ stands for a reference velocity. | ||
| + | Values for $\beta$ in the range of 1–10 are recommended for better convergence to the steady state at which the | ||
mass conservation is enforced. In addition, Equation ensures that $C$ does not reach zero at stagnation points | mass conservation is enforced. In addition, Equation ensures that $C$ does not reach zero at stagnation points | ||
that cause instabilities in pseudo-time, effecting convergence | that cause instabilities in pseudo-time, effecting convergence | ||
| + | |||
| + | Note, that for more complex simulation an internal iteration loops is required before marching in time. | ||
| + | |||
| + | |||
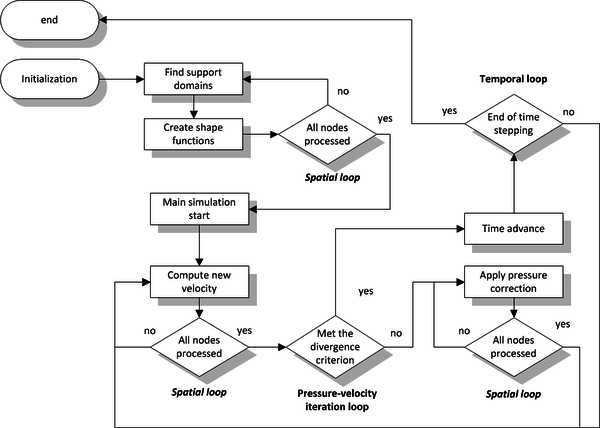
| + | <figure id="ACM"> | ||
| + | [[File:ACM BlockDiagram.png|600px]] | ||
| + | <caption>Scheme of the ACM algorithm </caption> | ||
| + | </figure> | ||
== Explicit/Implicit pressure calculation == | == Explicit/Implicit pressure calculation == | ||
Applying divergence on \ref{NavierStokes} yields | Applying divergence on \ref{NavierStokes} yields | ||
| − | \[\nabla \cdot \frac{\partial \b{v}}{\partial t}+\nabla \cdot (\b{v}\cdot \nabla )\b{v}=-\frac{1}{\rho }{{\nabla }^{2}} | + | \[\nabla \cdot \frac{\partial \b{v}}{\partial t}+\nabla \cdot (\b{v}\cdot \nabla )\b{v}=-\frac{1}{\rho }{{\nabla }^{2}}p+\nabla \cdot \nu {{\nabla }^{2}}\b{v}+\nabla \cdot \b{f}\] |
| − | And since $\nabla \cdot \b{v}=0$ and we can change order in $\nabla \cdot \nabla^2$ and $ \nabla^2 \cdot \nabla$ | + | And since $\nabla \cdot \b{v}=0$ and we can change order in $\nabla \cdot \nabla^2$ and $ \nabla^2 \cdot \nabla$ equation simplifies to |
| − | \[\frac{1}{\rho }{{\nabla }^{2}} | + | \[\frac{1}{\rho }{{\nabla }^{2}}p=\nabla \cdot \b{f}-\nabla \cdot (\b{v}\cdot \nabla )\b{v}\] |
Now, we need boundary conditions that can be obtained by multiplying the equation with a boundary normal vector | Now, we need boundary conditions that can be obtained by multiplying the equation with a boundary normal vector | ||
| − | \[\b{\hat{n}}\cdot \left( \frac{\partial \b{v}}{\partial t}+(\b{v}\cdot \nabla )\b{v} \right)=\b{\hat{n}}\cdot \left( -\frac{1}{\rho }\nabla | + | \[\b{\hat{n}}\cdot \left( \frac{\partial \b{v}}{\partial t}+(\b{v}\cdot \nabla )\b{v} \right)=\b{\hat{n}}\cdot \left( -\frac{1}{\rho }\nabla p+\nu {{\nabla }^{2}}\b{v}+\b{f} \right)\cdot \b{\hat{n}}\] |
| − | \[\frac{\partial | + | \[\frac{\partial p}{\partial \b{\hat{n}}}=\left( \nu {{\nabla }^{2}}\b{v}+\b{f}-\frac{\partial \b{v}}{\partial t}-(\b{v}\cdot\nabla ) \b{v} \right)\cdot \b{\hat{n}}\] |
Note that using tangential boundary vector gives equivalent BCs | Note that using tangential boundary vector gives equivalent BCs | ||
| − | \[\frac{\partial | + | \[\frac{\partial p}{\partial \b{\hat{t}}}=\left( \nu {{\nabla }^{2}}\b{v}+\b{f}-\frac{\partial \b{v}}{\partial t}-(\b{v}\cdot\nabla ) \b{v} \right)\cdot \b{\hat{t}}\] |
For no-slip boundaries BCs simplify to | For no-slip boundaries BCs simplify to | ||
| − | \[\frac{\partial | + | \[\frac{\partial p}{\partial \b{\hat{n}}}=\left( \nu {{\nabla }^{2}}\b{v}+\b{f} \right)\cdot \b{\hat{n}}\] |
Otherwise an appropriate expression regarding the velocity can be written, i.e. write full and taken in account velocity BCs. For example, Neumann velocity $\frac{\partial u}{\partial x}=0$ in 2D | Otherwise an appropriate expression regarding the velocity can be written, i.e. write full and taken in account velocity BCs. For example, Neumann velocity $\frac{\partial u}{\partial x}=0$ in 2D | ||
| − | \[\frac{\partial | + | \[\frac{\partial p}{\partial x}=\left( \nu {{\nabla }^{2}}u + {{f}_{x}}-\frac{\partial u}{\partial t}+v\frac{\partial u}{\partial y} \right)\] |
| − | Note that you allready know everything about the velocity and thus you can compute all the terms | + | Note that you allready know everything about the velocity and thus you can compute all the terms explicitly. |
So the procedure is: | So the procedure is: | ||
| − | + | ||
| − | + | * Compute Navier Stokes either explicitly or implicitly | |
| − | + | * Solve pressure equations with computed velocities | |
| + | * March in time | ||
Basic boundary conditions | Basic boundary conditions | ||
| − | Wall: $\b{v}=0$, \[\frac{\partial | + | Wall: $\b{v}=0$, \[\frac{\partial p}{\partial \hat{n}}=\left( \nabla \cdot \left( \nu \nabla \b{v} \right)+\b{f} \right)\cdot \hat{n}\] |
| − | Inlet: $\b{v}=\b{a}$, \[\frac{\partial | + | Inlet: $\b{v}=\b{a}$, \[\frac{\partial p}{\partial \hat{n}}=\left( \nabla \cdot \left( \nu \nabla \b{v} \right)+\b{f}-\nabla \cdot (\rho \b{v}\b{v})-\rho \frac{\partial \b{v}}{\partial t} \right)\cdot \hat{n}\] |
| − | Above system can be linearized (advection term) and | + | Above system can be linearized (advection term) and solved either explicitly or implicitly. |
Further reading: | Further reading: | ||
| − | + | ||
| − | + | W. D. Henshaw, A fourth-order accurate method for the incompressible Navier–Stokes equations on overlapping grids, J. Comput. Phys. 113, 13 (1994) | |
| + | |||
| + | J. C. Strikwerda, Finite difference methods for the Stokes and Navier–Stokes equations, SIAM J. Sci. Stat. | ||
Comput. 5(1), 56 (1984) | Comput. 5(1), 56 (1984) | ||
| − | == Explicit Pressure correction | + | == Explicit Pressure correction == |
Another possibility is to solve pressure correction equation. Again Consider the momentum equation and mass continuity and discretize it explicitly | Another possibility is to solve pressure correction equation. Again Consider the momentum equation and mass continuity and discretize it explicitly | ||
| − | \[\frac{{{\b{v}}_{2}}-{{\b{v}}_{1}}}{\Delta t}=-\frac{1}{\rho }\nabla {{ | + | \[\frac{{{\b{v}}_{2}}-{{\b{v}}_{1}}}{\Delta t}=-\frac{1}{\rho }\nabla {{p}_{1}}-({{\b{v}}_{1}}\nabla )\cdot {{\b{v}}_{1}}+\nu {{\nabla }^{2}}{{\b{v}}_{1}}+\b{f}\] |
| − | Computed velocity | + | Computed velocity obviously does not satisfy the mass contunity and therefore let’s call it intermediate velocity. Intermediate velocity is calculated from guessed pressure and old velocity values. |
| − | \[{{\b{v}}^{ | + | \[{{\b{v}}^{inter}}=\b{v}_1 + \Delta t\left( -\frac{1}{\rho }\nabla {{p}_{1}}-({{\b{v}}_{1}}\nabla )\cdot {{\b{v}}_{1}}+\nu {{\nabla }^{2}}{{\b{v}}_{1}}+\b{f} \right)\] |
| − | + | A correction term is added that drives velocity to divergence free field | |
| + | \[\nabla \cdot ({{\b{v}}^{inter}}+{{\b{v}}^{corr}})=0 \qquad \to \qquad \nabla \cdot {{\b{v}}^{inter}}=-\nabla \cdot {{\b{v}}^{corr}}\] | ||
| − | \[ | + | Velocity correction is affected only by effect of pressure correction. This fact is obvious due to all terms except gradient of pressure on the right side of equation are constant. |
| + | \[{{\b{v}}^{corr}}=-\frac{\Delta t}{\rho }\nabla {{p}^{corr}} \] | ||
| − | + | Note that corrected velocity also satisfies boundary conditions | |
| − | \[{{\ | + | \[\b{v}^{iter}+\b{v}^{corr}=\b{v}^{BC}\] |
| − | + | Applying divergence and we get '''pressure correction poisson equation'''. | |
| − | \[\,{{\nabla }^{2}}{{ | + | \[\,{{\nabla }^{2}}{{p}^{corr}}\,=\frac{\rho }{\Delta t}\nabla \cdot {{\mathbf{v}}^{iter}}\,\] |
| + | |||
| + | Boundary conditions can be obtained by mulitplying the equation with a unit normal vector $\b{\hat{n}}$ | ||
| + | \[\frac{\Delta t}{\rho }\frac{\partial {p}^{corr}}{\partial \b{\hat{n}}} = \b{\hat{n}} \cdot \left(\b{v}^{iter} - \b{v}^{BC} \right) \] | ||
| + | The most straightforward approach, for dirichlet BCs, is to take into account velocity boundary condition in computation of intermediate velocity, and clearly in such cases, pressure boundary condition simplifies to | ||
| + | \[\frac{\partial p^{corr}}{\partial \b{\hat{n}}} = 0 \] | ||
| + | As ${{\b{v}}^{\operatorname{int}er}}={{\b{v}}^{BC}}$ . Another option is to explicitely compute intermediate velocity also on boundaries and then correct it through pressure correction. | ||
| + | |||
| + | The pressure poisson equation is, at given boundary conditions, defined only up to a constant. One solution is to select a node and set it to a constant, e.g. p(0, 0) = 0, however much more stable approach is to enforce solution with additional condition, also referred to as a regularization | ||
| + | \[\int_{\Omega }^{{}}{pd}\Omega =0\] | ||
| + | \[\,{{\nabla }^{2}}{{p}^{corr}}\,-\alpha =\frac{\rho }{\Delta t}\nabla \cdot {{\b{v}}^{iter}}\,\] | ||
| + | Where $\alpha $ stands for Lagrange multiplier. Or in discrete form | ||
| + | \[\sum\limits_{i}{p\left( {{x}_{i}} \right)=0}\] | ||
| + | \[\b{Mp}-\alpha \b{1}=\frac{\rho }{\Delta t}\nabla \cdot {{\b{v}}^{iter}}\] | ||
| + | |||
| + | where $\b{M}$ holds Laplace shape functions, i.e. the discrete version of Laplace differential operator. | ||
| + | |||
| + | Solution of a system | ||
| − | + | \[\left[ \begin{matrix} | |
| − | \ | + | {{M}_{11}} & .. & {{M}_{1n}} & 1 \\ |
| − | + | .. & .. & .. & 1 \\ | |
| − | \ | + | {{M}_{n1}} & ... & {{M}_{nn}} & 1 \\ |
| + | 1 & 1 & 1 & 0 \\ | ||
| + | \end{matrix} \right]\left[ \begin{matrix} | ||
| + | {{p}_{1}} \\ | ||
| + | ... \\ | ||
| + | {{p}_{n}} \\ | ||
| + | \alpha \\ | ||
| + | \end{matrix} \right]=\frac{\rho }{\Delta t}\left[ \begin{matrix} | ||
| + | \nabla \cdot \b{v}_{_{1}}^{\text{iter}} \\ | ||
| + | ... \\ | ||
| + | \nabla \cdot \b{v}_{n}^{\text{iter}} \\ | ||
| + | 0 \\ | ||
| + | \end{matrix} \right]\] | ||
| + | Gives us a solution of pressure correction. | ||
== CBS Algorithm == | == CBS Algorithm == | ||
| − | With | + | With explicit temporal discretization problem is formulated as |
| − | \[\b{\hat{v}}={{\b{v}}_{0}}+\Delta t\left( -\nabla {{ | + | \[\b{\hat{v}}={{\b{v}}_{0}}+\Delta t\left( -\nabla {{p}_{0}}+\frac{1}{Re}{{\nabla }^{2}}{{\b{v}}_{0}}-\nabla \cdot ({{\b{v}}_{0}}{{\b{v}}_{0}}) \right)\] |
| − | \[ | + | \[p={{p}_{0}}-\xi \Delta {{t}_{F}}\nabla \b{\hat{v}}+\xi \Delta {{t}_{F}}\Delta t{{\nabla }^{2}}{{\overset{\scriptscriptstyle\frown}{P}}_{0}},\] |
| − | where $\b{\hat{v}} | + | where $\b{\hat{v}}$, $\Delta t$, $\xi$ and $\Delta t_F$ stand for intermediate velocity, time step, relaxation parameter, and artificial time step, respectively, and index 0 stands for previous time / iteration step. First, the intermediate velocity is computed from previous time step. Second, the velocity is driven towards solenoidal field by correcting the pressure. Note that no special boundary conditions for pressure are used, i.e., the pressure on boundaries is computed with the same approach as in the interior of the domain. In general, the internal iteration with an artificial time step is required until the divergence of the velocity field is not below required criteria. However, if one is interested only in a steady-state solution, the internal iteration can be skipped and $\Delta t$ equals $\Delta {{t}_{F}}$. Without internal stepping the transient of the solution is distorted by artificial compressibility effect. This approach is also known as ACM with Characteristics-based discretization of continuity equation, where the relaxation parameter relates to the artificial speed of sound [35]. |
The relaxation parameter should be set between 1-10, lower number more stable solution. | The relaxation parameter should be set between 1-10, lower number more stable solution. | ||
| Line 137: | Line 195: | ||
And also dimensional form | And also dimensional form | ||
| − | \[ | + | \[p={{p}_{0}}-{{C}^{2}}\Delta {{t}_{F}}\rho \nabla \b{\hat{v}}+{{C}^{2}}\Delta {{t}_{F}}\Delta t{{\nabla }^{2}}{{p}_{0}},\] |
Where C is speed of sound [m/s] | Where C is speed of sound [m/s] | ||
| − | == Numerical examples | + | == The Stream Function - Vorticity Approach == |
| + | |||
| + | In two dimensions, the Navier–Stokes equations can be expressed using the | ||
| + | stream function $\psi$ and the vorticity $\omega$ in place of the primitive variables $u$, $v$, and | ||
| + | $p$. This involves the elimination of the pressure $p$, thus yielding one dependent | ||
| + | variable less. In three dimensions, however, this formulation leads to six unknowns | ||
| + | rather than four (in primitive variables), which makes this approach less attractive | ||
| + | for that case. | ||
| + | |||
| + | In the following, we briefly derive the resulting two-dimensional equations for | ||
| + | $\psi$ and $\omega$. We begin by considering the momentum equations: | ||
| + | \begin{align} | ||
| + | \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}& = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right) + g_x \\ | ||
| + | \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}& = -\frac{1}{\rho}\frac{\partial p}{\partial y} + \nu \left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\right) + g_y | ||
| + | \end{align} | ||
| + | from which we can eliminate the pressure by differentiating the first equation by $y$ and the second by $x$, subtracting the second from the first and then substituting the definition for the vorticity $\omega = \partial u / \partial y - \partial v / \partial x$. In this manner we obtain the equation: | ||
| + | \[\frac{\partial \omega}{\partial t} + \frac{\partial u}{\partial x} \omega + u \frac{\partial \omega}{\partial x} + \frac{\partial v}{\partial y}\omega + v \frac{\partial \omega}{\partial y} = \nu \left(\frac{\partial^2 \omega}{\partial x^2} + \frac{\partial^2 \omega}{\partial y^2}\right) + \left(\frac{\partial g_x}{\partial y} - \frac{\partial g_y}{\partial x}\right)\] | ||
| + | |||
| + | We can get rid of the terms containing $\partial u / \partial x$ and $\partial v / \partial y$ by using the continuity equation \eqref{contuinity}. Finally using the definition for the stream function $\partial \psi / \partial y = u$ and $\partial \psi / \partial x = -v$ we can transform the above equation to what is known as the ''vorticity transport equation'': | ||
| + | \begin{equation} | ||
| + | \frac{\partial \omega}{\partial t} + \frac{\partial \psi}{\partial y}\frac{\partial \omega}{\partial x} - \frac{\partial \psi}{\partial x}\frac{\partial \omega}{\partial y} = \nu \Delta \omega + \left(\frac{\partial g_x}{\partial y} - \frac{\partial g_y}{\partial x}\right) | ||
| + | \label{vorticity_transport} | ||
| + | \end{equation} | ||
| + | |||
| + | Another equation is obtained by inserting the definition of the stream function into that of the vorticity: | ||
| + | \[\omega = \frac{\partial u}{\partial y} - \frac{\partial v}{\partial x} = \frac{\partial}{\partial y}\left(\frac{\partial \psi}{\partial y}\right) + \frac{\partial }{\partial x}\left(\frac{\partial \psi}{\partial x}\right) = \Delta \psi\] | ||
| + | leading to the ''Poisson equation for the stream function'' | ||
| + | \begin{equation} | ||
| + | \Delta \psi = \omega | ||
| + | \label{poisson_stream} | ||
| + | \end{equation} | ||
| + | |||
| + | The two equations (\ref{vorticity_transport}) and (\ref{poisson_stream}) form a nonlinear coupled system of equations in which pressure has been eliminated and in which the continuity equation has been satisfied automatically. | ||
| + | |||
| + | = Numerical examples = | ||
* [[Lid driven cavity]] | * [[Lid driven cavity]] | ||
| + | * [[Burgers' equation]] | ||
* [[de Vahl Davis natural convection test]] | * [[de Vahl Davis natural convection test]] | ||
| + | * [[Natural convection in 3D irregular domain]] | ||
| + | * [[Natural convection from heated cylinder]] | ||
| + | * [[Natural convection between concentric cylinders]] | ||
| + | * [[Non-Newtonian fluid]] | ||
Latest revision as of 14:23, 2 March 2024
Contents
Introduction
Computational fluid dynamics (CFD) is a field of a great interest among researchers in many fields of science, e.g. studying mathematical fundaments of numerical methods, developing novel physical models, improving computer implementations, and many others. Pushing the limits of all involved fields of science helps community to deepen the understanding of several natural and technological phenomena. Weather forecast, ocean dynamics, water transport, casting, various energetic studies, etc., are just few examples where fluid dynamics plays a crucial role. The core problem of the CFD is solving the Navier-Stokes Equation or its variants, e.g. Darcy or Brinkman equation for flow in porous media. Here, we discuss basic algorithms for solving CFD problems. Check reference list on the main page for more details about related work.
Long story short, we want to solve \begin{equation} \frac{\partial \b{v}}{\partial t}+\nabla \cdot ( \rho \b{vv}) = -\nabla p+ \nabla(\mu \nabla\b{v})+\b{f} \label{NavierStokes} \end{equation} also known as a Navier-Stokes equation.
Note that the $\b{v}\b{v}$ stands for the tensor or dyadic product \[ \b{v}\b{v} = \b{v}\otimes\b{v} = \b{v}\b{v}^\T = \left[ \begin{matrix} {{v}_{1}}{{v}_{1}} & \cdots & {{v}_{1}}{{v}_{n}} \\ \vdots & \ddots & \vdots \\ {{v}_{n}}{{v}_{1}} & \cdots & {{v}_{n}}{{v}_{n}} \\ \end{matrix} \right]\]
Combining equation \ref{NavierStokes} and mass contiunity equation \begin{equation} \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho {\bf{u}}) = 0. \end{equation}
simplifies advection term into (see [1] for derivation)
\[\frac{\partial \left( \rho \b{v} \right)}{\partial t}+\nabla \cdot \left( \rho \b{vv} \right)=\frac{\partial \left( \rho \b{v} \right)}{\partial t}+(\rho \b{v}\cdot \nabla )\cdot \b{v}. \]
An example of advection term in 2D would therefore be \[\left( \b{v}\cdot \nabla \right)\b{v}=\left( \left( \begin{matrix} u \\ v \\ \end{matrix} \right) \cdot \left( \begin{matrix} \frac{\partial }{\partial x} \\ \frac{\partial }{\partial y} \\ \end{matrix} \right) \right)\left( \begin{matrix} u \\ v \\ \end{matrix} \right)=\left( \begin{matrix} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} \\ u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} \\ \end{matrix} \right)\]
In many cases we are interested in the incompressible fluids (Ma<0.3), reducing the continuity equation to
\begin{equation}
\nabla \cdot \b{v}=0
\label{contuinity}
\end{equation}
The goal of CFD is to solve system \ref{NavierStokes} and \ref{contuinity}. It is obvious that a special treatment will be needed to couple both equations. In the following discussion we cover some basic approaches, how this can be accomplished.
Solutions algorithms
Artificial compressibility method
The simplest, completely explicit approach, is an artificial compressibility method (ACM), where a compressibility term is included in the mass continuity \[\frac{\partial \b{v}}{\partial t}+(\b{v}\cdot\nabla )\b{v}=-\frac{1}{\rho }\nabla p+\nu {{\nabla }^{2}}\b{v}+\b{f}\] \[\frac{ 1 }{ \rho } \frac{\partial \rho }{\partial t}+\nabla \cdot \b{v}=0\] \[\frac{ 1 }{ \rho } \frac{\partial \rho }{\partial p}\frac{\partial p}{\partial t}+\nabla \cdot \b{v}=0\] Now, the above system can be solved directly.
The addition of the time derivative of the pressure term physically means that waves of finite speed (the propagation of which depends on the magnitude of the ACM) are introduced into the flow field as a mean to distribute the pressure within the domain. In a true incompressible flow, the pressure field is affected instantaneously throughout the whole domain. In ACM there is a time delay between the flow disturbance and its effect on the pressure field. Upon rearranging the equation yields \[\frac{\partial p}{\partial t}+\rho {{C}^{2}}\nabla \cdot \b{v}=0\] where the continuity equation is perturbed by the quantity $\frac{\partial p}{\partial t}$ denominated herein as the AC parameter/artificial sound speed recognized by $C$ [m/s] - speed of sound \[\frac{1}{C^2}=\frac{\partial \rho }{\partial p}\] Or in other words \[C^2=\left( \frac{\partial p}{\partial \rho}\right)_S\] where $\rho$ is the density of the material. It follows, by replacing partial derivatives, that the isentropic compressibility can be expressed as: \[\beta =\frac{1}{\rho {{C}^{2}}}\] The evaluation of the local ACM parameter in incompressible flows is inspired by the speed of sound computations in compressible flows (for instance, from the perfect gas law). However, in the incompressible flow situation, employing such a relation is difficult, but an artificial relation can be developed from the convective and diffusive velocities. Reverting to the justification of continuity modification, it can be immediately seen that the artificial sound speed must be sufficiently large to have a significant regularizing effect and at the same time must be as small as possible to minimizing perturbations on the incompressibility equation. Therefore, $C$ influences the convergence rate and stability of the solution method. In other words, assists in reducing large disparity in the eigenvalues, leading to a well-conditioned system. The $C$ can be estimated with
\[ C = \beta \max \left( \left|\b{v}\right|_2, \left|\b{v}_{ref}\right|_2 \right),\] where $\b{v}_{ref}$ stands for a reference velocity. Values for $\beta$ in the range of 1–10 are recommended for better convergence to the steady state at which the mass conservation is enforced. In addition, Equation ensures that $C$ does not reach zero at stagnation points that cause instabilities in pseudo-time, effecting convergence
Note, that for more complex simulation an internal iteration loops is required before marching in time.
Explicit/Implicit pressure calculation
Applying divergence on \ref{NavierStokes} yields \[\nabla \cdot \frac{\partial \b{v}}{\partial t}+\nabla \cdot (\b{v}\cdot \nabla )\b{v}=-\frac{1}{\rho }{{\nabla }^{2}}p+\nabla \cdot \nu {{\nabla }^{2}}\b{v}+\nabla \cdot \b{f}\]
And since $\nabla \cdot \b{v}=0$ and we can change order in $\nabla \cdot \nabla^2$ and $ \nabla^2 \cdot \nabla$ equation simplifies to \[\frac{1}{\rho }{{\nabla }^{2}}p=\nabla \cdot \b{f}-\nabla \cdot (\b{v}\cdot \nabla )\b{v}\] Now, we need boundary conditions that can be obtained by multiplying the equation with a boundary normal vector \[\b{\hat{n}}\cdot \left( \frac{\partial \b{v}}{\partial t}+(\b{v}\cdot \nabla )\b{v} \right)=\b{\hat{n}}\cdot \left( -\frac{1}{\rho }\nabla p+\nu {{\nabla }^{2}}\b{v}+\b{f} \right)\cdot \b{\hat{n}}\] \[\frac{\partial p}{\partial \b{\hat{n}}}=\left( \nu {{\nabla }^{2}}\b{v}+\b{f}-\frac{\partial \b{v}}{\partial t}-(\b{v}\cdot\nabla ) \b{v} \right)\cdot \b{\hat{n}}\]
Note that using tangential boundary vector gives equivalent BCs \[\frac{\partial p}{\partial \b{\hat{t}}}=\left( \nu {{\nabla }^{2}}\b{v}+\b{f}-\frac{\partial \b{v}}{\partial t}-(\b{v}\cdot\nabla ) \b{v} \right)\cdot \b{\hat{t}}\] For no-slip boundaries BCs simplify to \[\frac{\partial p}{\partial \b{\hat{n}}}=\left( \nu {{\nabla }^{2}}\b{v}+\b{f} \right)\cdot \b{\hat{n}}\] Otherwise an appropriate expression regarding the velocity can be written, i.e. write full and taken in account velocity BCs. For example, Neumann velocity $\frac{\partial u}{\partial x}=0$ in 2D \[\frac{\partial p}{\partial x}=\left( \nu {{\nabla }^{2}}u + {{f}_{x}}-\frac{\partial u}{\partial t}+v\frac{\partial u}{\partial y} \right)\] Note that you allready know everything about the velocity and thus you can compute all the terms explicitly.
So the procedure is:
- Compute Navier Stokes either explicitly or implicitly
- Solve pressure equations with computed velocities
- March in time
Basic boundary conditions Wall: $\b{v}=0$, \[\frac{\partial p}{\partial \hat{n}}=\left( \nabla \cdot \left( \nu \nabla \b{v} \right)+\b{f} \right)\cdot \hat{n}\] Inlet: $\b{v}=\b{a}$, \[\frac{\partial p}{\partial \hat{n}}=\left( \nabla \cdot \left( \nu \nabla \b{v} \right)+\b{f}-\nabla \cdot (\rho \b{v}\b{v})-\rho \frac{\partial \b{v}}{\partial t} \right)\cdot \hat{n}\]
Above system can be linearized (advection term) and solved either explicitly or implicitly.
Further reading:
W. D. Henshaw, A fourth-order accurate method for the incompressible Navier–Stokes equations on overlapping grids, J. Comput. Phys. 113, 13 (1994)
J. C. Strikwerda, Finite difference methods for the Stokes and Navier–Stokes equations, SIAM J. Sci. Stat. Comput. 5(1), 56 (1984)
Explicit Pressure correction
Another possibility is to solve pressure correction equation. Again Consider the momentum equation and mass continuity and discretize it explicitly \[\frac{{{\b{v}}_{2}}-{{\b{v}}_{1}}}{\Delta t}=-\frac{1}{\rho }\nabla {{p}_{1}}-({{\b{v}}_{1}}\nabla )\cdot {{\b{v}}_{1}}+\nu {{\nabla }^{2}}{{\b{v}}_{1}}+\b{f}\] Computed velocity obviously does not satisfy the mass contunity and therefore let’s call it intermediate velocity. Intermediate velocity is calculated from guessed pressure and old velocity values. \[{{\b{v}}^{inter}}=\b{v}_1 + \Delta t\left( -\frac{1}{\rho }\nabla {{p}_{1}}-({{\b{v}}_{1}}\nabla )\cdot {{\b{v}}_{1}}+\nu {{\nabla }^{2}}{{\b{v}}_{1}}+\b{f} \right)\] A correction term is added that drives velocity to divergence free field \[\nabla \cdot ({{\b{v}}^{inter}}+{{\b{v}}^{corr}})=0 \qquad \to \qquad \nabla \cdot {{\b{v}}^{inter}}=-\nabla \cdot {{\b{v}}^{corr}}\]
Velocity correction is affected only by effect of pressure correction. This fact is obvious due to all terms except gradient of pressure on the right side of equation are constant. \[{{\b{v}}^{corr}}=-\frac{\Delta t}{\rho }\nabla {{p}^{corr}} \]
Note that corrected velocity also satisfies boundary conditions \[\b{v}^{iter}+\b{v}^{corr}=\b{v}^{BC}\] Applying divergence and we get pressure correction poisson equation. \[\,{{\nabla }^{2}}{{p}^{corr}}\,=\frac{\rho }{\Delta t}\nabla \cdot {{\mathbf{v}}^{iter}}\,\]
Boundary conditions can be obtained by mulitplying the equation with a unit normal vector $\b{\hat{n}}$ \[\frac{\Delta t}{\rho }\frac{\partial {p}^{corr}}{\partial \b{\hat{n}}} = \b{\hat{n}} \cdot \left(\b{v}^{iter} - \b{v}^{BC} \right) \] The most straightforward approach, for dirichlet BCs, is to take into account velocity boundary condition in computation of intermediate velocity, and clearly in such cases, pressure boundary condition simplifies to \[\frac{\partial p^{corr}}{\partial \b{\hat{n}}} = 0 \] As ${{\b{v}}^{\operatorname{int}er}}={{\b{v}}^{BC}}$ . Another option is to explicitely compute intermediate velocity also on boundaries and then correct it through pressure correction.
The pressure poisson equation is, at given boundary conditions, defined only up to a constant. One solution is to select a node and set it to a constant, e.g. p(0, 0) = 0, however much more stable approach is to enforce solution with additional condition, also referred to as a regularization \[\int_{\Omega }^{{}}{pd}\Omega =0\] \[\,{{\nabla }^{2}}{{p}^{corr}}\,-\alpha =\frac{\rho }{\Delta t}\nabla \cdot {{\b{v}}^{iter}}\,\] Where $\alpha $ stands for Lagrange multiplier. Or in discrete form \[\sum\limits_{i}{p\left( {{x}_{i}} \right)=0}\] \[\b{Mp}-\alpha \b{1}=\frac{\rho }{\Delta t}\nabla \cdot {{\b{v}}^{iter}}\]
where $\b{M}$ holds Laplace shape functions, i.e. the discrete version of Laplace differential operator.
Solution of a system
\[\left[ \begin{matrix} {{M}_{11}} & .. & {{M}_{1n}} & 1 \\ .. & .. & .. & 1 \\ {{M}_{n1}} & ... & {{M}_{nn}} & 1 \\ 1 & 1 & 1 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{p}_{1}} \\ ... \\ {{p}_{n}} \\ \alpha \\ \end{matrix} \right]=\frac{\rho }{\Delta t}\left[ \begin{matrix} \nabla \cdot \b{v}_{_{1}}^{\text{iter}} \\ ... \\ \nabla \cdot \b{v}_{n}^{\text{iter}} \\ 0 \\ \end{matrix} \right]\] Gives us a solution of pressure correction.
CBS Algorithm
With explicit temporal discretization problem is formulated as \[\b{\hat{v}}={{\b{v}}_{0}}+\Delta t\left( -\nabla {{p}_{0}}+\frac{1}{Re}{{\nabla }^{2}}{{\b{v}}_{0}}-\nabla \cdot ({{\b{v}}_{0}}{{\b{v}}_{0}}) \right)\] \[p={{p}_{0}}-\xi \Delta {{t}_{F}}\nabla \b{\hat{v}}+\xi \Delta {{t}_{F}}\Delta t{{\nabla }^{2}}{{\overset{\scriptscriptstyle\frown}{P}}_{0}},\] where $\b{\hat{v}}$, $\Delta t$, $\xi$ and $\Delta t_F$ stand for intermediate velocity, time step, relaxation parameter, and artificial time step, respectively, and index 0 stands for previous time / iteration step. First, the intermediate velocity is computed from previous time step. Second, the velocity is driven towards solenoidal field by correcting the pressure. Note that no special boundary conditions for pressure are used, i.e., the pressure on boundaries is computed with the same approach as in the interior of the domain. In general, the internal iteration with an artificial time step is required until the divergence of the velocity field is not below required criteria. However, if one is interested only in a steady-state solution, the internal iteration can be skipped and $\Delta t$ equals $\Delta {{t}_{F}}$. Without internal stepping the transient of the solution is distorted by artificial compressibility effect. This approach is also known as ACM with Characteristics-based discretization of continuity equation, where the relaxation parameter relates to the artificial speed of sound [35].
The relaxation parameter should be set between 1-10, lower number more stable solution.
And also dimensional form
\[p={{p}_{0}}-{{C}^{2}}\Delta {{t}_{F}}\rho \nabla \b{\hat{v}}+{{C}^{2}}\Delta {{t}_{F}}\Delta t{{\nabla }^{2}}{{p}_{0}},\]
Where C is speed of sound [m/s]
The Stream Function - Vorticity Approach
In two dimensions, the Navier–Stokes equations can be expressed using the stream function $\psi$ and the vorticity $\omega$ in place of the primitive variables $u$, $v$, and $p$. This involves the elimination of the pressure $p$, thus yielding one dependent variable less. In three dimensions, however, this formulation leads to six unknowns rather than four (in primitive variables), which makes this approach less attractive for that case.
In the following, we briefly derive the resulting two-dimensional equations for $\psi$ and $\omega$. We begin by considering the momentum equations: \begin{align} \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y}& = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right) + g_x \\ \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y}& = -\frac{1}{\rho}\frac{\partial p}{\partial y} + \nu \left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\right) + g_y \end{align} from which we can eliminate the pressure by differentiating the first equation by $y$ and the second by $x$, subtracting the second from the first and then substituting the definition for the vorticity $\omega = \partial u / \partial y - \partial v / \partial x$. In this manner we obtain the equation: \[\frac{\partial \omega}{\partial t} + \frac{\partial u}{\partial x} \omega + u \frac{\partial \omega}{\partial x} + \frac{\partial v}{\partial y}\omega + v \frac{\partial \omega}{\partial y} = \nu \left(\frac{\partial^2 \omega}{\partial x^2} + \frac{\partial^2 \omega}{\partial y^2}\right) + \left(\frac{\partial g_x}{\partial y} - \frac{\partial g_y}{\partial x}\right)\]
We can get rid of the terms containing $\partial u / \partial x$ and $\partial v / \partial y$ by using the continuity equation \eqref{contuinity}. Finally using the definition for the stream function $\partial \psi / \partial y = u$ and $\partial \psi / \partial x = -v$ we can transform the above equation to what is known as the vorticity transport equation: \begin{equation} \frac{\partial \omega}{\partial t} + \frac{\partial \psi}{\partial y}\frac{\partial \omega}{\partial x} - \frac{\partial \psi}{\partial x}\frac{\partial \omega}{\partial y} = \nu \Delta \omega + \left(\frac{\partial g_x}{\partial y} - \frac{\partial g_y}{\partial x}\right) \label{vorticity_transport} \end{equation}
Another equation is obtained by inserting the definition of the stream function into that of the vorticity: \[\omega = \frac{\partial u}{\partial y} - \frac{\partial v}{\partial x} = \frac{\partial}{\partial y}\left(\frac{\partial \psi}{\partial y}\right) + \frac{\partial }{\partial x}\left(\frac{\partial \psi}{\partial x}\right) = \Delta \psi\] leading to the Poisson equation for the stream function \begin{equation} \Delta \psi = \omega \label{poisson_stream} \end{equation}
The two equations (\ref{vorticity_transport}) and (\ref{poisson_stream}) form a nonlinear coupled system of equations in which pressure has been eliminated and in which the continuity equation has been satisfied automatically.