Difference between revisions of "Convection Diffusion equation"
(→Time dependent 2D case) |
(→References) |
||
| (27 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Before moving to more complex numerical examples | + | Before moving to more complex numerical examples we solve the convection diffusion equation in different regimes. |
| − | |||
A 2D diffusion equation in its dimensionless form is considered: | A 2D diffusion equation in its dimensionless form is considered: | ||
| − | \begin{align} | + | \begin{align} |
| − | \frac{\partial u}{\partial t} - \alpha \nabla^2u | + | \frac{\partial u}{\partial t} - \alpha \nabla^2u + \b{v}\cdot \nabla u = q, & \qquad (x, y)\in \Omega, \label{eq.diffu}\\ |
| − | |||
u(x,y,t) = \overline{u}(x,y,t), & \qquad (x,y) \in \Gamma_D,\label{eq.bc_diffu}\\ | u(x,y,t) = \overline{u}(x,y,t), & \qquad (x,y) \in \Gamma_D,\label{eq.bc_diffu}\\ | ||
u(x,y,t),_n = \overline{g}(x,y,t), & \qquad (x,y) \in \Gamma_N, \label{eq.mixed.bc_diffu}\\ | u(x,y,t),_n = \overline{g}(x,y,t), & \qquad (x,y) \in \Gamma_N, \label{eq.mixed.bc_diffu}\\ | ||
| Line 89: | Line 87: | ||
[[File:quarter_diffusion.png|397px]][[File:poisson_weird1.png|397px]][[File:poisson_weird2.png|195px]] | [[File:quarter_diffusion.png|397px]][[File:poisson_weird1.png|397px]][[File:poisson_weird2.png|195px]] | ||
| − | == | + | == Convection Diffusion == |
| + | |||
| + | The following example problem is adapted from [http://servidor.demec.ufpr.br/CFD/bibliografia/Ferziger%20Peric%20-%20Computational%20Methods%20for%20Fluid%20Dynamics,%203rd%20Ed%20-%202002.pdf Ferziger & Perič (2002) (pages 82-86)]. | ||
| + | |||
| + | [[File:Screenshot_2016-11-28_11-05-03.png|400px]] | ||
| + | |||
| + | We now consider the problem of a scalar quantity transported in a known velocity field $\b{v}$. The velocity field is given by | ||
| + | \[\b{u} = (u_x,u_y) = (x, -y),\] | ||
| + | which represents the flow near a stagnation point $(x,y) = (0,0)$. The streamlines $xy=\mathrm{const.}$ and change direction with respect to the Cartesian grid. The convection-diffusion equation (also known as the scalar transport equation) is to be solved with the following boundary conditions: | ||
| + | * $u = 0$ along the north (inlet) boundary; | ||
| + | * linear variation $u= (1 - y)$ along the west boundary ($x = 0$); | ||
| + | * symmetry condition on the south boundary; | ||
| + | * zero gradient at the east (outlet) boundary. | ||
| + | The parameter $\alpha$ is the diffusivity for the scalar quantity $u$. The problem and boundary conditions are schematically represented in below figure together with The solutions obtained by Ferziger and Perić. | ||
| + | |||
| + | [[File:Screenshot_2016-11-28_11-07-44.png|470px]] [[File:fvm_convection.png|600px]] | ||
| + | |||
| + | The meshless solution is obtained on regular point arrangements of sizes 100 × 100 and 300 × 300, for the 2 cases of diffusivity $\alpha = 0.01$ and $\alpha = 0.001$, respectively. For comparison we have plotted the contour lines at the same intervals as the original authors of this example. The basis functions are the 5 monomials $1$, $x$, $y$, $x^2$, $y^2$. | ||
| + | |||
| + | == Electrostatics Poisson's equation == | ||
| + | A special case of convection diffusion equation is also a Poisson's equation. | ||
| + | Our next example is taken from the [http://www.freefem.org/ff++/ftp/freefem++doc.pdf FreeFem++ manual (page 235)]. | ||
| + | |||
| + | Assuming there is no current and the charge distribution is time independent, the electric field $\b{E}$ satisfies | ||
| + | \begin{equation}\label{eq:electrostatics} | ||
| + | \b{\nabla}\cdot\b{E} = \frac{\rho}{\epsilon}, \quad \b{\nabla} \times \b{E} = 0 | ||
| + | \end{equation} | ||
| + | where $\rho$ is the charge density and $\epsilon$ is the permittivity. If we introduce an electrostatics potential $\phi$ such that | ||
| + | \begin{equation} | ||
| + | \b{E} = -\b{\nabla}\phi, | ||
| + | \end{equation} | ||
| + | we can insert it into the first equation in (\ref{eq:electrostatics}) resulting in Poisson's equation | ||
| + | \begin{equation}\label{eq:poisson} | ||
| + | \b{\nabla}^2 \phi = -\frac{\rho}{\epsilon}. | ||
| + | \end{equation} | ||
| + | In the absence of unpaired electric charge equation (\ref{eq:poisson}) becomes Laplace's equation | ||
| + | \begin{equation} | ||
| + | \b{\nabla}^2 \phi = 0 | ||
| + | \end{equation} | ||
| + | |||
| + | We now solve this equation for a circular enclosure with two rectangular holes. The boundary of the circular enclosure is held at constant potential $0$ V. The two rectangular holes are held at constant potentials $+1$ V and $-1$ V, respectively. | ||
| + | |||
| − | + | [[File:electrostatics.png|500px]] | |
| + | == 3D cases == | ||
| − | + | First, the behavior of the method is tested on the regular case. The equation $\nabla^2 u = -\pi^2 \sin(\pi x) \sin(\pi y) \sin(\pi z)$ is solved on domain $[0, 1/2]^3$, | |
| − | + | where sides with at least one coordinate 0 have Dirichet BCs $u = 0$ and other sides have Neumann conditions $\frac{\partial u}{\partial \vec{n}} = 0$. The convergence of MLSM in two different setups | |
| − | + | is shown below. Max error is taken for error measure. | |
| − | |||
| − | |||
| − | |||
| + | [[File:pois3d_neu_poiss.png|500px]] | ||
| − | |||
| − | |||
| − | |||
| + | And few more 3D cases that are not part of any serious analysis and were made only for fun. | ||
| − | + | A 3-dimensional example, where a CAD model for aluminium heat sink is | |
discretized to obtain the domain description. | discretized to obtain the domain description. | ||
| − | Heat equation with $\alpha = 9.7 \cdot 10^{-5 | + | Heat equation with $\alpha = 9.7 \cdot 10^{-5}$, with no heat generation, i.e. $q = 0$, with Dirichlet boundary conditions |
| − | $u = | + | $u = 100 ^\circ C$ on the bottom surface and |
| − | $u = | + | $u = 20 ^\circ C$ everywhere else. |
[[File:heat_sink_cad.png|440px]][[File:heat_sink_sol1.png|440px]][[File:heat_sink_sol2.png|175px]] | [[File:heat_sink_cad.png|440px]][[File:heat_sink_sol1.png|440px]][[File:heat_sink_sol2.png|175px]] | ||
| Line 121: | Line 157: | ||
[[File:beef_1.png|350px]][[File:beef_3.png|350px]][[File:beef_2.png|350px]] | [[File:beef_1.png|350px]][[File:beef_3.png|350px]][[File:beef_2.png|350px]] | ||
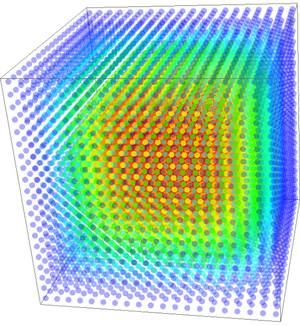
| − | And finally, steady state temperature profile of a triceratops | + | And finally, steady state temperature profile of a triceratops and ... a box. |
| − | [[File:triceratops.jpg|400px]] | + | [[File:triceratops.jpg|400px]][[File:diffusion3d.png|300px]] |
'''We will add more serious 3D results as soon as we get motivated to prepare them, hopefully with some awesome project''' | '''We will add more serious 3D results as soon as we get motivated to prepare them, hopefully with some awesome project''' | ||
| Line 132: | Line 168: | ||
* Slak, J., Kosec, G.. Detection of heart rate variability from a wearable differential ECG device., MIPRO 2016, 39th International Convention, 2016, Opatija, Croatia, ISSN 1847-3938, pp 450-455. | * Slak, J., Kosec, G.. Detection of heart rate variability from a wearable differential ECG device., MIPRO 2016, 39th International Convention, 2016, Opatija, Croatia, ISSN 1847-3938, pp 450-455. | ||
| − | '''This list might be incomplete, check also reference on the [[Main Page]].''' | + | '''This list might be incomplete, check also reference on the [[Medusa | Main Page]].''' |
Latest revision as of 11:06, 9 July 2019
Before moving to more complex numerical examples we solve the convection diffusion equation in different regimes. A 2D diffusion equation in its dimensionless form is considered: \begin{align} \frac{\partial u}{\partial t} - \alpha \nabla^2u + \b{v}\cdot \nabla u = q, & \qquad (x, y)\in \Omega, \label{eq.diffu}\\ u(x,y,t) = \overline{u}(x,y,t), & \qquad (x,y) \in \Gamma_D,\label{eq.bc_diffu}\\ u(x,y,t),_n = \overline{g}(x,y,t), & \qquad (x,y) \in \Gamma_N, \label{eq.mixed.bc_diffu}\\ u(x,y,t) = u_0, & \qquad t=0,\label{eq.ic_diffu} \end{align} where $(x,y)$ are spatial coordinates, $t$ is time, $u(x, y, t)$ is the unknown solution, $ \Omega$, and $ \Gamma_D$ and $ \Gamma_N$ are the global domain with Dirichlet boundary and Neumann boundary, $\overline{u}$ and $\overline{g}$ are the prescribed Dirichlet and Neumann boundary values and $u(x,y,0)=u_0$ is the known initial condition.
In following discussion we present some solutions and test we did while coding our library. Please refer to our repository for full set of latest examples and tests
Contents
Steady state 1D case
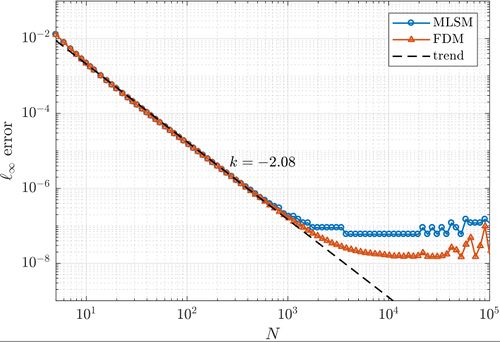
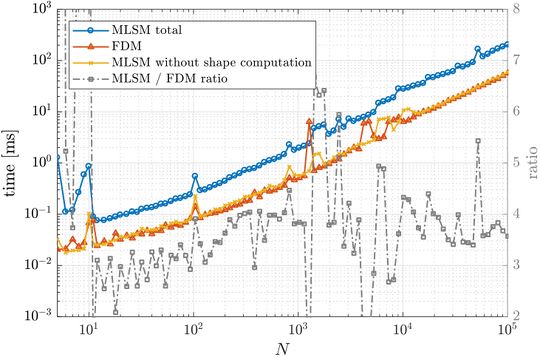
First, a simple one dimensional case is tackled to assess basic properties of presented solution method. Consider the problem \begin{align} u''(x) &= \sin(x), \quad x \in (0, 1) \nonumber \\ u(0) &= 0 \label{eq:neu1d} \\ u'(1) &= 0 \nonumber \end{align} with analytical solution \begin{equation} u(x) = x \cos 1 - \sin x. \end{equation} We solve the problem with MLSM using 3 support nodes and 3 monomials $\{1, x, x^2\}$ as basis functions on a regularly distributed nodes. This setup of MLSM is theoretically equivalent to the Finite Difference Method (FDM) and therefore it is worth implementing also standard FDM to compare results and execution times. The error between the actual solution $u$ and the approximate solution $\hat{u}$ is measured in $\ell_\infty$ norm, \begin{equation} \|u - \hat{u}\|_{\ell_\infty} = \max_{x\in X} | u(x) - \hat{u}(x)|, \label{eq:linf-err} \end{equation} where $X$ is the set of all points in the domain. The problem can be solved with below code. Note, that the code is the same for 1,2 and 3D cases
1 for (int i : domain.internal()) {
2 op.lap(M, i, 1.0); // Equation.
3 rhs(i) = std::sin(domain.positions[i][0]);
4 }
5 op.value(M, left, 1.0); // Left BC.
6 op.neumann(M, right, {1}, 1.0); // Right BC.
7 VectorXd solution = M.lu().solve(rhs);
As expected, MLSM is slower due to computation of shape functions, which are known in advance in FDM. However, counting that as part of the preprocessing and measuring only the part equivalent to FDM, it can be seen that the execution times for FDM and MLSM are the same for all practical purposes.
Time dependent 2D case
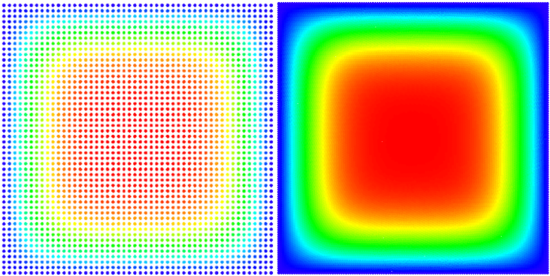
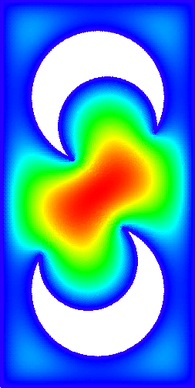
We solved the equation on a square $\Omega = [0, a] \times [0, a]$ with Dirichlet boundary conditions $ \left. u\right|_{\partial \Omega} = 0 $ and initial state $ u(t = 0) = 1$. An analytical solution for this domain is known \begin{equation} u(\vec{p}, t) = \sum_{\substack{n=1 \\ n \text{ odd}}}^\infty\sum_{\substack{m=1 \\ m \text{ odd}}}^\infty \frac{1}{\pi^2} \frac{16 a^2}{nm} \sin\left(\frac{\pi n}{a}p_x\right) \sin\left(\frac{\pi m}{a}p_y\right) e^{-\frac{\pi^2 (n^2+m^2)}{a^2}t} \end{equation}
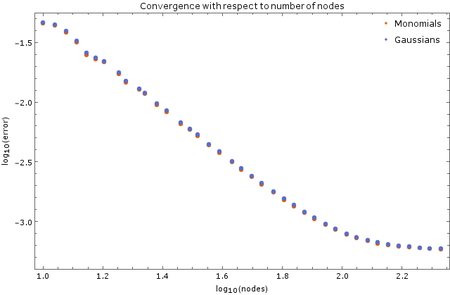
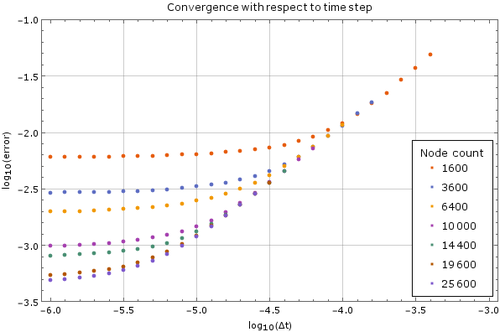
Temperature contour polot after $t = 0.05$ and convergence regarding the number of nodes
We tested the method with a fixed time step of $ \Delta t = 1\cdot 10^{-5}$ on a unit square ($a = 1$). Monomial basis of $6$ monomials was used and $12$ closest nodes counted as support for each node in one setup and in another 5 Guassians on 5 suport nodes. After more than $250$ nodes of discretization in each dimension the method diverges, which is expected. The stability criterion for diffusion equation in two dimensions is $\Delta t \leq \frac{1}{4} \Delta x^2$, where $\Delta x$ is the spatial discretization step in one dimension. In our case, at $250$ nodes per side, the right hand side yields $\frac{1}{4}\cdot\frac{1}{250}\cdot\frac{1}{250} = 4\times 10^{-6}$, so our method is stable within the expected region.
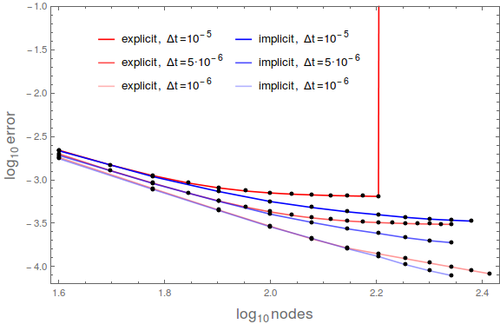
Convergence with respect to number of time steps and comaprios between implicit and explicit solution
And 1/4 case, where we have mixed Neumann/Dirichlet boundary condition due to the symmetry together with some more weird domains, just to have some fun ...
Convection Diffusion
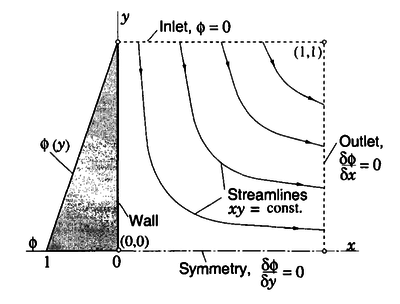
The following example problem is adapted from Ferziger & Perič (2002) (pages 82-86).
We now consider the problem of a scalar quantity transported in a known velocity field $\b{v}$. The velocity field is given by \[\b{u} = (u_x,u_y) = (x, -y),\] which represents the flow near a stagnation point $(x,y) = (0,0)$. The streamlines $xy=\mathrm{const.}$ and change direction with respect to the Cartesian grid. The convection-diffusion equation (also known as the scalar transport equation) is to be solved with the following boundary conditions:
- $u = 0$ along the north (inlet) boundary;
- linear variation $u= (1 - y)$ along the west boundary ($x = 0$);
- symmetry condition on the south boundary;
- zero gradient at the east (outlet) boundary.
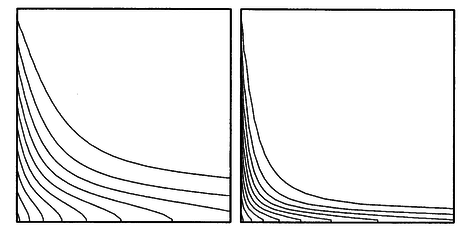
The parameter $\alpha$ is the diffusivity for the scalar quantity $u$. The problem and boundary conditions are schematically represented in below figure together with The solutions obtained by Ferziger and Perić.
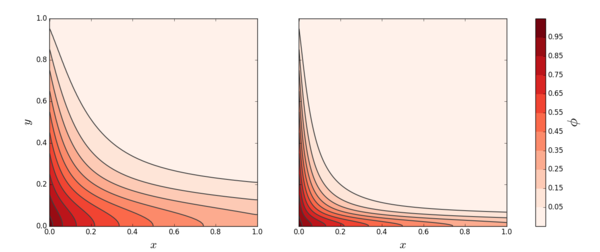
The meshless solution is obtained on regular point arrangements of sizes 100 × 100 and 300 × 300, for the 2 cases of diffusivity $\alpha = 0.01$ and $\alpha = 0.001$, respectively. For comparison we have plotted the contour lines at the same intervals as the original authors of this example. The basis functions are the 5 monomials $1$, $x$, $y$, $x^2$, $y^2$.
Electrostatics Poisson's equation
A special case of convection diffusion equation is also a Poisson's equation. Our next example is taken from the FreeFem++ manual (page 235).
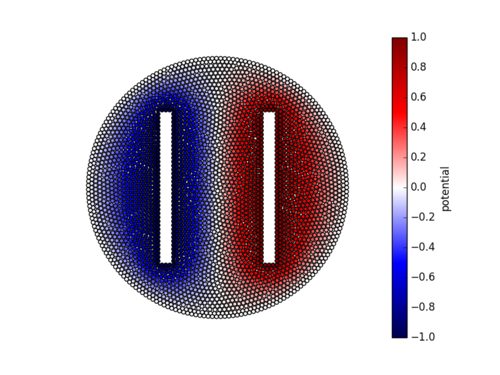
Assuming there is no current and the charge distribution is time independent, the electric field $\b{E}$ satisfies \begin{equation}\label{eq:electrostatics} \b{\nabla}\cdot\b{E} = \frac{\rho}{\epsilon}, \quad \b{\nabla} \times \b{E} = 0 \end{equation} where $\rho$ is the charge density and $\epsilon$ is the permittivity. If we introduce an electrostatics potential $\phi$ such that \begin{equation} \b{E} = -\b{\nabla}\phi, \end{equation} we can insert it into the first equation in (\ref{eq:electrostatics}) resulting in Poisson's equation \begin{equation}\label{eq:poisson} \b{\nabla}^2 \phi = -\frac{\rho}{\epsilon}. \end{equation} In the absence of unpaired electric charge equation (\ref{eq:poisson}) becomes Laplace's equation \begin{equation} \b{\nabla}^2 \phi = 0 \end{equation}
We now solve this equation for a circular enclosure with two rectangular holes. The boundary of the circular enclosure is held at constant potential $0$ V. The two rectangular holes are held at constant potentials $+1$ V and $-1$ V, respectively.
3D cases
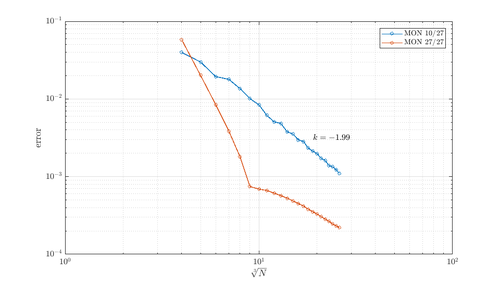
First, the behavior of the method is tested on the regular case. The equation $\nabla^2 u = -\pi^2 \sin(\pi x) \sin(\pi y) \sin(\pi z)$ is solved on domain $[0, 1/2]^3$, where sides with at least one coordinate 0 have Dirichet BCs $u = 0$ and other sides have Neumann conditions $\frac{\partial u}{\partial \vec{n}} = 0$. The convergence of MLSM in two different setups is shown below. Max error is taken for error measure.
And few more 3D cases that are not part of any serious analysis and were made only for fun.
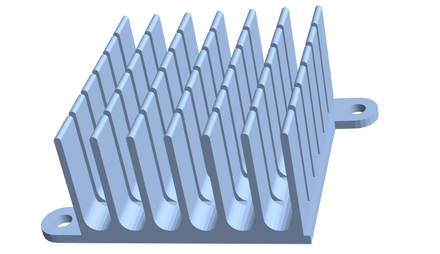
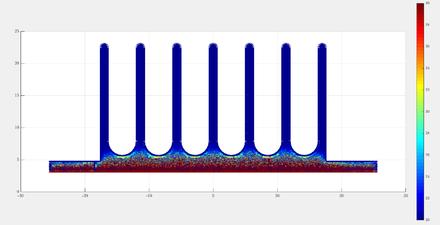
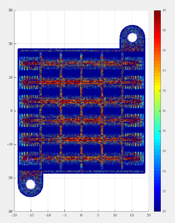
A 3-dimensional example, where a CAD model for aluminium heat sink is discretized to obtain the domain description. Heat equation with $\alpha = 9.7 \cdot 10^{-5}$, with no heat generation, i.e. $q = 0$, with Dirichlet boundary conditions $u = 100 ^\circ C$ on the bottom surface and $u = 20 ^\circ C$ everywhere else.
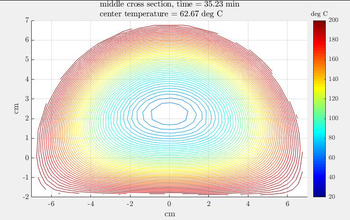
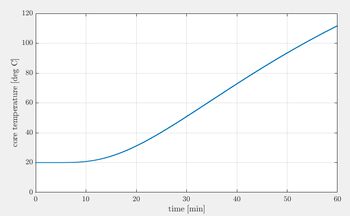
Next, example is simulation of baking Beef Wellington, where we followed therecipe. The simple 3D model is discretized with 70490 points and simulated for one hour with 1 s time step. The initial temperature is set to 20 deg C, the oven temperature is set to 200 deg C. Heat diffusivity of beef is found in the literature, the dimensions are 34 x 14 x 9 cm.
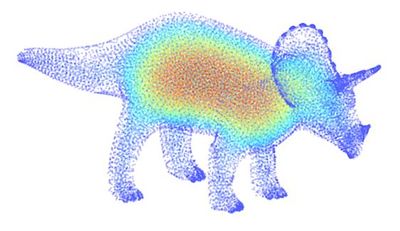
And finally, steady state temperature profile of a triceratops and ... a box.
We will add more serious 3D results as soon as we get motivated to prepare them, hopefully with some awesome project
References
- Trobec R., Kosec G., Šterk M., Šarler B., Comparison of local weak and strong form meshless methods for 2-D diffusion equation. Engineering analysis with boundary elements. 2012;36:310-321; manuscript
- robec R., Kosec G., Parallel Scientific Computing, ISBN: 978-3-319-17072-5 (Print) 978-3-319-17073-2.
- Slak, J., Kosec, G.. Detection of heart rate variability from a wearable differential ECG device., MIPRO 2016, 39th International Convention, 2016, Opatija, Croatia, ISSN 1847-3938, pp 450-455.
This list might be incomplete, check also reference on the Main Page.