Difference between revisions of "Ghost nodes (theory)"
From Medusa: Coordinate Free Mehless Method implementation
| Line 1: | Line 1: | ||
| + | <figure id="fig:tests"> | ||
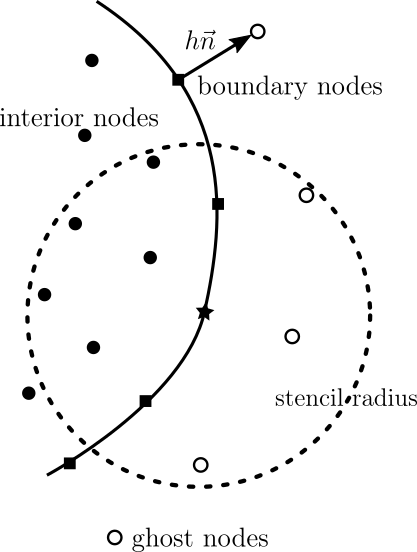
| + | [[File:ghost.png|417px|thumb|upright=2|alt=Ghost nodes schema.|<caption>Ghost node configuration at the domain boundary.</caption>]] | ||
| + | </figure> | ||
| + | |||
Ghost nodes are a technique for discretizing (mostly) Neumann boundary conditions in PDEs. | Ghost nodes are a technique for discretizing (mostly) Neumann boundary conditions in PDEs. | ||
| Line 9: | Line 13: | ||
| − | |||
| − | |||
| − | |||
=== Explicit version === | === Explicit version === | ||
TODO Jure | TODO Jure | ||
Revision as of 10:44, 17 May 2019
Ghost nodes are a technique for discretizing (mostly) Neumann boundary conditions in PDEs.
Introduction
Ghost are a technique used for disretizing Neumann boundary conditions in FDM. To be able to use the central difference for first derivative, additional point, called ghost point, is introduced outside the domain boudanry. The unknown function value at the ghost node is added as a variable. At the boundary node, the Neumann condition is enforced, as well as the equation itself (two equations for two unknowns, the ghost and the boundary function value).
Meshless setting (implicit)
Consider the problem $\mathcal{L}u = f$ with Neumann boundary conditions $\frac{\partial u}{\partial n} = g$ on some portion of the boundary.
Explicit version
TODO Jure