Difference between revisions of "Coupled domains"
| Line 42: | Line 42: | ||
inner.fill(fill_engine, h); // this is the inner circle | inner.fill(fill_engine, h); // this is the inner circle | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | The snippet above shows how to add the the nodes on the common boundary to the inner domain. The normals of the shared boundary nodes belonging to the inner domain must point into the opposite direction as the normals belonging to the shared boundary nodes in the outer domain. After this is done insides of both domains are filled. | + | The snippet above shows how to add the the nodes on the common boundary to the inner domain. The normals of the shared boundary nodes belonging to the inner domain must point into the opposite direction as the normals belonging to the shared boundary nodes in the outer domain. After this is done insides of both domains are filled. The size of the matrix $M$ of the system must be equal to the sum of points in the inner and outer domains. |
| + | <syntaxhighlight lang="c++" line> | ||
| + | Eigen::SparseMatrix<double, Eigen::RowMajor> M(N_inner+N_outer, N_inner+N_outer); | ||
| + | Eigen::VectorXd rhs(N_inner+N_outer); | ||
| + | </syntaxhighlight> | ||
| + | Additionaly we must construct two sets of storages, and two sets of operators, one for each domain. The operators of the outer domain must be offset by the number of nodes in the inner domain, this assures that the operators are writing values in the right part of the matrix $M$. | ||
| + | <syntaxhighlight lang="c++" line> | ||
| + | |||
| + | auto storage_inner = inner.computeShapes<sh::lap|sh::d1>(wls); | ||
| + | auto storage_outer = outer.computeShapes<sh::lap|sh::d1>(wls); | ||
| + | |||
| + | auto op_inner = storage_inner.implicitOperators(M, rhs); | ||
| + | auto op_outer = storage_outer.implicitOperators(M, rhs); | ||
| + | op_outer.setRowOffset(N_inner); | ||
| + | op_outer.setColOffset(N_inner); | ||
| + | </syntaxhighlight> | ||
| + | On the shared boundary we must reserve two slots for the equality of values of $u$ and $v$, and the appropriate number of slots to store two shapes due to equality normal derivatives of $u$ and $v$. | ||
| + | <syntaxhighlight lang="c++" line> | ||
| + | Range<int> reserve = storage_inner.supportSizes() + storage_outer.supportSizes(); | ||
| + | // Compute row sizes on the common boundary | ||
| + | for (int i : common_bnd) { | ||
| + | reserve[outer_to_inner[i]] = 2; // equality of values needs 2 slots | ||
| + | reserve[N_inner+i] = storage_inner.supportSize(outer_to_inner[i]) + storage_outer.supportSize(i); // equality of fluxes needs two shapes | ||
| + | } | ||
| + | M.reserve(reserve); | ||
| + | </syntaxhighlight> | ||
| + | Finally we can implement the case, being careful to write in the appropriate parts of the matrix when dealing with shared points | ||
| + | <syntaxhighlight lang="c++" line> | ||
| + | for (int i : inner.interior()) { | ||
| + | -lam1*op_inner.lap(i) = q0; // laplace in interior of inner domain | ||
| + | } | ||
| + | for (int i : outer.interior()) { | ||
| + | lam2*op_outer.lap(i) = 0; // laplace in interior of outer domain | ||
| + | } | ||
| + | for (int i : outer_bnd) { | ||
| + | op_outer.value(i) = 0.0; // outer Dirichlet BC | ||
| + | } | ||
| + | for (int i : common_bnd) { | ||
| + | int j = outer_to_inner[i]; | ||
| + | op_inner.value(j) + -1.0*op_outer.value(i, -N_inner+j) = 0.0; // continuity over shared boundary | ||
| + | lam1*op_inner.neumann(j, inner.normal(j), N_inner+i) + lam2*op_outer.neumann(i, outer.normal(i)) = 0.0; // flux | ||
| + | } | ||
| + | |||
| + | </syntaxhighlight> | ||
Revision as of 16:47, 18 April 2019
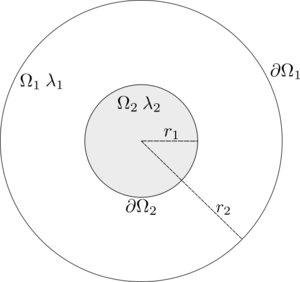
In this example we will show how one can solve coupled problems with Medusa library. We will solve the stationary heat equation on concentric circles where the thermal conductivity $\lambda$ is different for each circle. The inner circle will be heated up, while the outside temperature will be held at zero.
In mathematical terms, we want to solve the system \begin{align*} -\Delta v = q_0 \qquad &\text{on} \quad \Omega_2 \\ \Delta u = 0 \qquad &\text{on} \quad \Omega_1 \end{align*}
With boundary conditions \begin{align*} u = 0 \qquad &\text{on} \quad \partial \Omega_1 \\ u = v \qquad &\text{on} \quad \partial \Omega_2 \\ \frac{\partial u}{\partial n_1} = \frac{\partial v}{\partial n_2} \qquad &\text{on} \quad \partial \Omega_2 \\ \end{align*} We will see that the task is quite simple using Medusa, first we create the domains $\Omega_1$ and $\Omega_2$
1 BallShape<Vec2d> inner_shape(0, r1);
2 BallShape<Vec2d> outer_circle(0, r2);
3 auto outer_shape = outer_circle - inner_shape;
4
5 DomainDiscretization<Vec2d> outer = outer_shape.discretizeBoundaryWithStep(h);
6 DomainDiscretization<Vec2d> inner(inner_shape);
7
8 // Indices of nodes in outer domain that constitute outer and common boundary.
9 auto common_bnd = outer.positions().filter([=](const Vec2d& p) { return std::abs(p.norm() - r1) < 1e-5; });
10 auto outer_bnd = outer.positions().filter([=](const Vec2d& p) { return std::abs(p.norm() - r2) < 1e-5; });
In the code above, we constructed two BallShapes and calculated their difference, giving us the shape of an annulus. We use the annulus shape to obtain the outer domain discretization, and the BallShape with the smaller radius to construct the inner domain discretization. Some care needs to be given to filling the domains, we need to be careful because we want the domains to share the nodes on the boundary $\partial \Omega_2$. Notice that as we discretized the boundary of the annulus we already filled both $\partial \Omega_1$ and $\partial \Omega_2$. Hence, we filter the boundary nodes of the outer domain into the outer boundary and the common boundary, this will prove useful later on.
1 // Maps node indices of outer domain to their corresponding indices in the inner domain.
2 Range<int> outer_to_inner(outer.size(), -1);
3 for (int i : common_bnd) {
4 int idx = inner.addBoundaryNode(outer.pos(i), -2, -outer.normal(i));
5 outer_to_inner[i] = idx;
6 }
7
8 GeneralFill<Vec2d> fill_engine; fill_engine.seed(1);
9 outer.fill(fill_engine, h); // this is the annulus
10 inner.fill(fill_engine, h); // this is the inner circle
The snippet above shows how to add the the nodes on the common boundary to the inner domain. The normals of the shared boundary nodes belonging to the inner domain must point into the opposite direction as the normals belonging to the shared boundary nodes in the outer domain. After this is done insides of both domains are filled. The size of the matrix $M$ of the system must be equal to the sum of points in the inner and outer domains.
1 Eigen::SparseMatrix<double, Eigen::RowMajor> M(N_inner+N_outer, N_inner+N_outer);
2 Eigen::VectorXd rhs(N_inner+N_outer);
Additionaly we must construct two sets of storages, and two sets of operators, one for each domain. The operators of the outer domain must be offset by the number of nodes in the inner domain, this assures that the operators are writing values in the right part of the matrix $M$.
1 auto storage_inner = inner.computeShapes<sh::lap|sh::d1>(wls);
2 auto storage_outer = outer.computeShapes<sh::lap|sh::d1>(wls);
3
4 auto op_inner = storage_inner.implicitOperators(M, rhs);
5 auto op_outer = storage_outer.implicitOperators(M, rhs);
6 op_outer.setRowOffset(N_inner);
7 op_outer.setColOffset(N_inner);
On the shared boundary we must reserve two slots for the equality of values of $u$ and $v$, and the appropriate number of slots to store two shapes due to equality normal derivatives of $u$ and $v$.
1 Range<int> reserve = storage_inner.supportSizes() + storage_outer.supportSizes();
2 // Compute row sizes on the common boundary
3 for (int i : common_bnd) {
4 reserve[outer_to_inner[i]] = 2; // equality of values needs 2 slots
5 reserve[N_inner+i] = storage_inner.supportSize(outer_to_inner[i]) + storage_outer.supportSize(i); // equality of fluxes needs two shapes
6 }
7 M.reserve(reserve);
Finally we can implement the case, being careful to write in the appropriate parts of the matrix when dealing with shared points
1 for (int i : inner.interior()) {
2 -lam1*op_inner.lap(i) = q0; // laplace in interior of inner domain
3 }
4 for (int i : outer.interior()) {
5 lam2*op_outer.lap(i) = 0; // laplace in interior of outer domain
6 }
7 for (int i : outer_bnd) {
8 op_outer.value(i) = 0.0; // outer Dirichlet BC
9 }
10 for (int i : common_bnd) {
11 int j = outer_to_inner[i];
12 op_inner.value(j) + -1.0*op_outer.value(i, -N_inner+j) = 0.0; // continuity over shared boundary
13 lam1*op_inner.neumann(j, inner.normal(j), N_inner+i) + lam2*op_outer.neumann(i, outer.normal(i)) = 0.0; // flux
14 }