Difference between revisions of "1D MLSM and FDM comparison"
(→Dirichlet case) |
(→Preliminaries) |
||
| (11 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
</math> | </math> | ||
| − | were analysed. Theoretically, [https://en.wikipedia.org/wiki/Finite_difference_method FDM] and MLSM should match completely. | + | were analysed. Theoretically, [https://en.wikipedia.org/wiki/Finite_difference_method FDM] and [[Meshless Local Strong Form Method (MLSM) | MLSM]] should match completely. |
This is practivaly demonstrated up to certain discretization level. | This is practivaly demonstrated up to certain discretization level. | ||
The interval <math>[0, 1]</math> was always discretized uniformly using $N$ nodes, <math>x_i = a+i h, h = (b-a)/N</math>. | The interval <math>[0, 1]</math> was always discretized uniformly using $N$ nodes, <math>x_i = a+i h, h = (b-a)/N</math>. | ||
| + | |||
| + | == Preliminaries == | ||
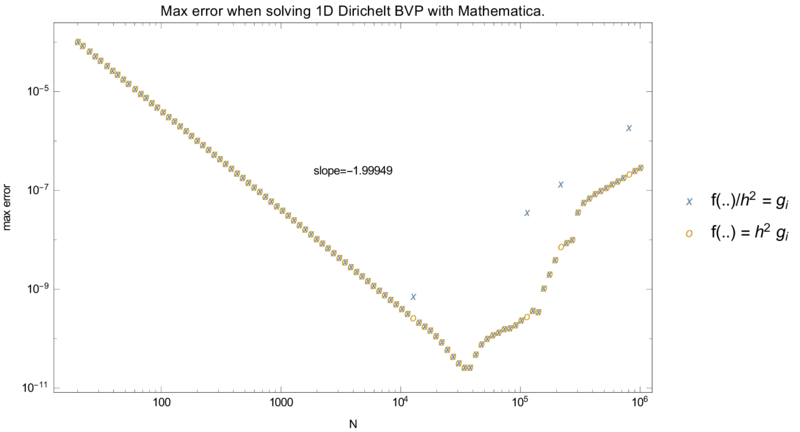
| + | When solving such problems one usually makes the disretization of the form <math>f''(x_i) \approx (f_{i-1} -2 f_i + f_{i+1}) / h^2</math>, | ||
| + | but when writing the system of equations, it is usually written as $f_{i-1} -2 f_i + f_{i+1} = h^2 g(x_i)$. | ||
| + | In the general MLSM formulation it is not possible to always do that and therefore we want to know if there are any numerical differences | ||
| + | between solving $f_{i-1} -2 f_i + f_{i+1} = h^2 g(x_i)$ and $(f_{i-1} -2 f_i + f_{i+1})_h^2 = g(x_i)$. No significant differences were noted. | ||
| + | |||
| + | [[File:dir2systems.png|800px]] | ||
== Dirichlet case == | == Dirichlet case == | ||
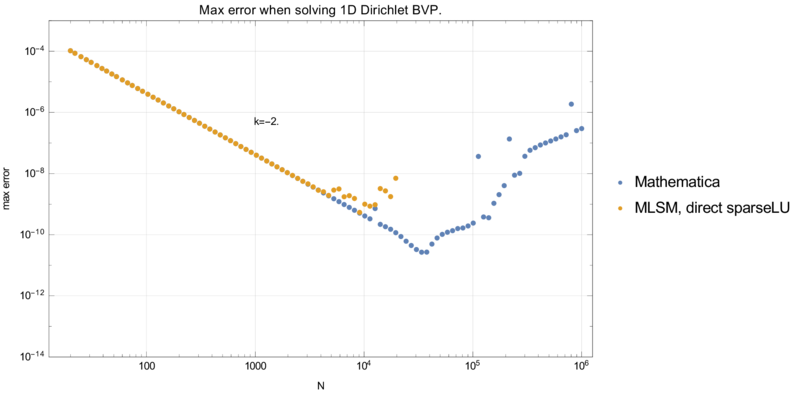
Precision and execution time are summarised in graphs below. | Precision and execution time are summarised in graphs below. | ||
| + | MSLM and Mathematica use $O(nN)$ time to build a matrix and solve the system. Additionally, MLSM uses $O(Nmn^2)$ to construct the shape functions. | ||
| + | The $O$ constant is close to 1 as all operations are basic arithemtic operations. Indded, in this case $n = m = 3$ and if we add this theoretical complexity of $27N$ | ||
| + | to Mathematica case, we fall directly in the MLSM case. | ||
[[File:dircmp.png|800px]][[File:dirtimecmp.png|800px]] | [[File:dircmp.png|800px]][[File:dirtimecmp.png|800px]] | ||
| Line 24: | Line 35: | ||
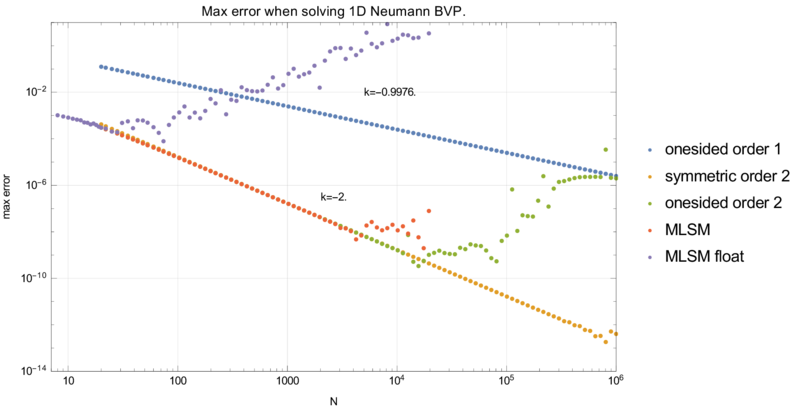
Three explored options are: | Three explored options are: | ||
| − | + | * onesided finite difference <math>f'(0) \approx (f_1 - f_0) / h</math> | |
| − | + | * symmetric finite difference <math>f'(0) \approx (f_1 - f_{-1}) / h</math> and normal discretization in node 0 <math>f''(0) \approx (f_1 - 2f_0 + f_{-1}) /h^2</math> | |
| − | + | * onesided double finite difference <math>f'(0) \approx (-3/2 f_0 + 2f_1 -1/2 f_2) / h</math> | |
| + | |||
| + | MLSM with support size $n = 3$ and three polynomial basis functions results in exactly the FDM method with onesided double finite difference approximation. | ||
| + | |||
| + | [[File:neucmp.png|800px]][[File:neutimecmp.png|800px]] | ||
| + | |||
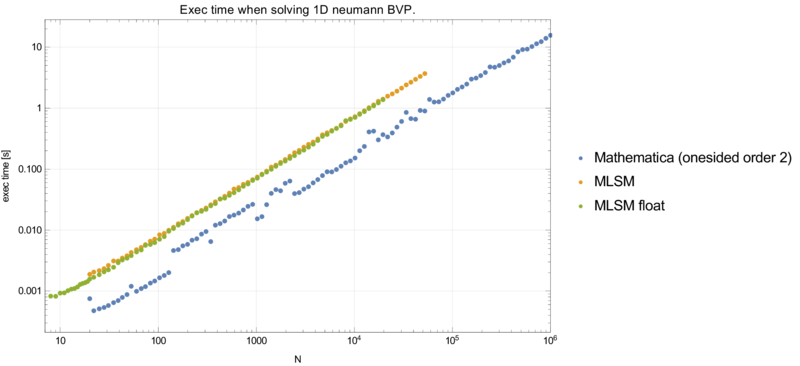
| + | The note on time complexity from the Dirichlet case apllies in this case as well. we can also see that nothing is to be gained from using only single precision. | ||
Latest revision as of 16:26, 20 June 2017
Different numerical approaches to solving a Dirichlet or Neumann problem
\(
\begin{align*}
\text{Dirichlet} && \text{Neumann} \\
f''(x) &= 2x^2+5 \text{ on } (0, 1) & f''(x) &= 2x^2+5 \text{ on } (0, 1) \\
f(0) &= 1 & f'(0) &= 1 \\
f(1) &= 1 & f(1) &= 1 \\
f(x) &= \frac{1}{6} \left(x^4+15 x^2-16 x+6\right) & f(x) &= \frac{1}{6} \left(x^4+15 x^2+6 x-16\right)
\end{align*}
\)
were analysed. Theoretically, FDM and MLSM should match completely. This is practivaly demonstrated up to certain discretization level.
The interval \([0, 1]\) was always discretized uniformly using $N$ nodes, \(x_i = a+i h, h = (b-a)/N\).
Preliminaries
When solving such problems one usually makes the disretization of the form \(f''(x_i) \approx (f_{i-1} -2 f_i + f_{i+1}) / h^2\), but when writing the system of equations, it is usually written as $f_{i-1} -2 f_i + f_{i+1} = h^2 g(x_i)$. In the general MLSM formulation it is not possible to always do that and therefore we want to know if there are any numerical differences between solving $f_{i-1} -2 f_i + f_{i+1} = h^2 g(x_i)$ and $(f_{i-1} -2 f_i + f_{i+1})_h^2 = g(x_i)$. No significant differences were noted.
Dirichlet case
Precision and execution time are summarised in graphs below. MSLM and Mathematica use $O(nN)$ time to build a matrix and solve the system. Additionally, MLSM uses $O(Nmn^2)$ to construct the shape functions. The $O$ constant is close to 1 as all operations are basic arithemtic operations. Indded, in this case $n = m = 3$ and if we add this theoretical complexity of $27N$ to Mathematica case, we fall directly in the MLSM case.
Neumann case
We have more that one possible disctretization of the Neumann BC in point 0. Three explored options are:
- onesided finite difference \(f'(0) \approx (f_1 - f_0) / h\)
- symmetric finite difference \(f'(0) \approx (f_1 - f_{-1}) / h\) and normal discretization in node 0 \(f''(0) \approx (f_1 - 2f_0 + f_{-1}) /h^2\)
- onesided double finite difference \(f'(0) \approx (-3/2 f_0 + 2f_1 -1/2 f_2) / h\)
MLSM with support size $n = 3$ and three polynomial basis functions results in exactly the FDM method with onesided double finite difference approximation.
The note on time complexity from the Dirichlet case apllies in this case as well. we can also see that nothing is to be gained from using only single precision.