Inertial effects on fluid flow in complex porous media
Porous media are everywhere. Fluid flow through them is of utmost importance for science, technology, and life, as the lungs and the arterial system may be in fact treated as porous systems. However, despite decades of research, there are still some fundamental problems that remain open and hinder our understanding of this phenomenon. One of them is how to link the microscopic flow, particularly through pores, with the macroscopic properties of the entire sample. For many decades a purely empirical Carman-Kozeny law has been employed to fill in this gap. This law binds two macroscopic characteristics of a porous medium: permeability (which measures the sample’s ability to let the fluid pass through it) and porosity (which measures the medium’s ability to store the fluid) with tortuosity – a characteristics of the flow itself that measures the irregularity of flow paths (its value increases as fluid paths deviate from straight lines). Despite the success of tortuosity as a parameter that allows us to quantify flow in porous structures, its use is presently limited to an empirical, material-dependent constant and the connection is conceptually based on behaviour in low-Reynolds number flows. Such an approach is unsatisfactory, as it neglects the physical nature of tortuosity, e.g. its dependency on inertial effects in the flow.

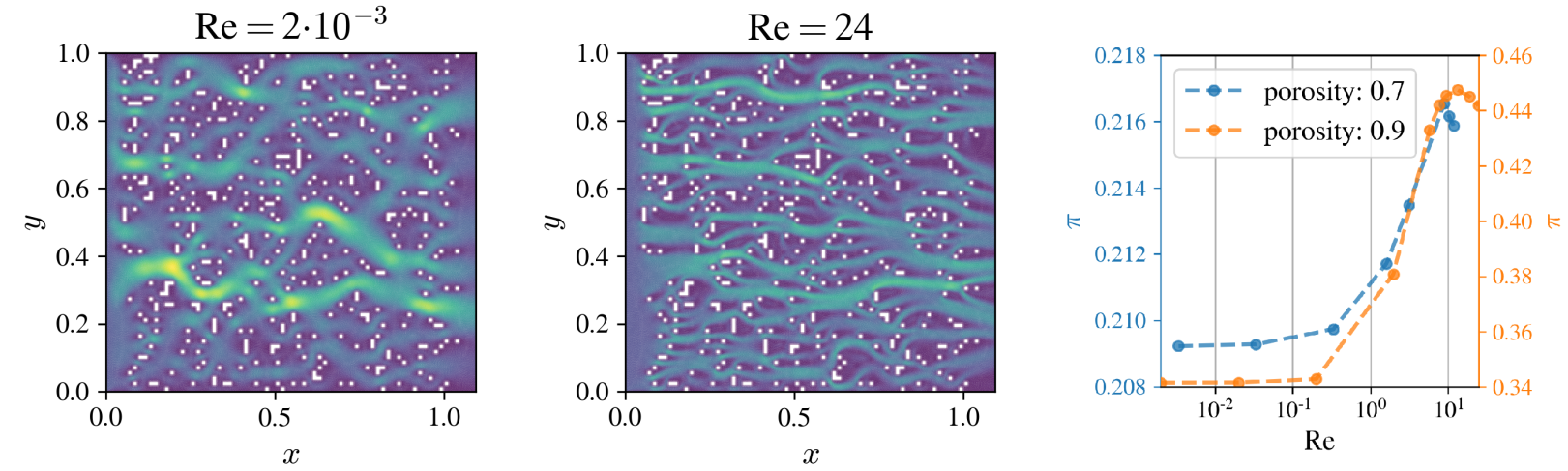
According to Abbas et al, “the relationship between the microstructure of a porous medium and the observed flow distribution is still a puzzle”. Dynamics of fluids is, for instance, of the frst importance to the oil industry interested in rocks permeability and oil droplets/ganglia extraction techniques+. The transport may be investigated either on the pore level or on the averaged macroscopic description. Due to the complex pore geometry, an experimental and numerical study in real media is not trivial. The fundamental problem is how to relate the microscopic scale of transport with the macroscopic physical properties of the real sample? The classical approach to the description of transport through porous media is Darcy’s Law that connects flux, viscosity and pressure gradient with permeability. To determine the permeability we use Carman-Kozeny law based on the capillary theory that describes the relationship between porosity and permeability with tortuosity of pores. Tortuosity is introduced to account for irregularities of pores geometry. It is the ratio between the effective length of flowing particle paths Le to the length of the system. If flow velocity increases enough, the inertial effects appear and linear Darcy Law doesn’t work anymore. The typical approach is to use the Forhheimer equation which, adds as additional terms in Darcy Law. In 1999 Andrade et. al showed the change in kinetic energy distribution resulting in the change of streamlines geometry in inertial flows. We suggest this will affect the tortuosity of the flow as well. One may ask how inertial effects influence tortuosity of the media? We want to address this manner and verify that tortuosity of porous media is not determined solely by geometry. Is tortuosity a feature of porous media geometry or does it depend on the transport phenomenon in question? How does flow-related tortuosity change if we increase the Reynolds number? How kinetic energy distribution in complex media depends on porosity? Is it possible to use Carman-Kozeny law with modifed tortuosity for inertial flows? To address these general questions we will investigate tortuosity and permeability in complex media of random and fractal nature at varying flow speeds. Flow speed change will result in a change of an inertial part of the Reynolds number. Our study will also raise the question about a proper defnition of length scale in Reynolds number in the porous medium. There is much inconsistency in the literature, where length scale L is taken as averaged grain size, pore size or even square root of permeability. Our study will reveal if numerical values of the Reynolds number in different classes of porous media indicate the same onset of inertial flows and agree with literature (Re=1-15 for the onset of inertial effects). If the difference is signifcant it will open a new research area with possible directions of reformulating the length scale defnition based on the geometric properties of the porous medium.
The project will be done in collaboration between two groups: one at the University of Wrocław (UWr) and the other at the Jožef Stefan Institute in Ljubljana (JSI). Its goal is studying pioneering problems in the field of basic fluid dynamics applied to porous media using modern numerical methods and simulations. Thanks to the knowledge and experience of both groups we will be able to provide new and reliable results.
P-Lab team
Polish team:
Sahrish Batool Naqvi, Dawid Strzelczyk, Damian Śnieżek and Maciej Matyka all from University of Wrocław
Funding