Execution on Intel® Xeon Phi™ co-processor

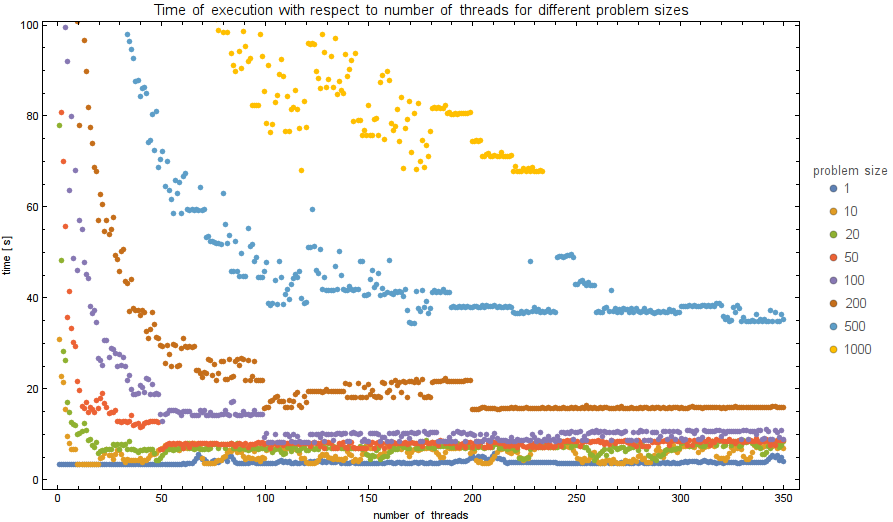
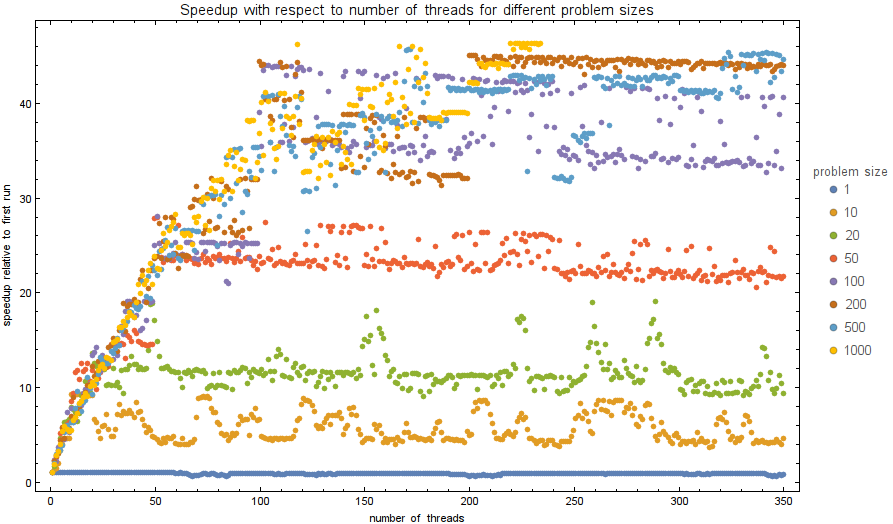
Speedup by parallelization

We tested the speedups on the Intel® Xeon Phi™ with the following code:

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #include <string.h>
 4 #include <assert.h>
 5 #include <omp.h>
 6 #include <math.h>
 7 
 8 int main(int argc, char *argv[]) {
 9     int numthreads;
10     int n;
11 
12     assert(argc == 3 && "args: numthreads n");
13     sscanf(argv[1], "%d", &numthreads);
14     sscanf(argv[2], "%d", &n);
15 
16     printf("Init...\n");
17     printf("Start (%d threads)...\n", numthreads);
18     printf("%d test cases\n", n);
19 
20     int m = 1000000;
21     double ttime = omp_get_wtime();
22 
23     int i;
24     double d = 0;
25 #pragma offload target(mic:0)
26     {
27 #pragma omp parallel for private (i) schedule(static) num_threads(numthreads)
28         for(i = 0; i < n; ++i) {
29             for(int j = 0; j < m; ++j) {
30                 d = sin(d) + 0.1 + j;
31                 d = pow(0.2, d)*j;
32             }
33         }
34     }
35     double time = omp_get_wtime() - ttime;
36     fprintf(stderr, "%d %d %.6f\n", n, numthreads, time);
37     printf("time: %.6f s\n", time);
38     printf("Done d = %.6lf.\n", d);
39 
40     return 0;
41 }

The code essentially distributes a problem of size $n\cdot m$ among numthreads cores, We tested the time of execution for $n$ from the set $\{1, 10, 20, 50, 100, 200, 500, 1000\}$ and numthreads from $1$ to $350$. The plots of exectuion times and performance speeups are shown below.

The code was compiled using:
icc -openmp -O3 -qopt-report=2 -qopt-report-phase=vec -o test test.cpp
without warnings or errors. Then, in order to offload to Intel Phi, user must be logged in as root:
sudo su
To run correctly, intel compiler and runtime variables must be sourced:
source /opt/intel/bin/compilervars.sh intel64
Finally, the code was tested using the following command, where test is the name of the compiled executable:
for n in 1 10 20 50 100 200 500 1000; do for nt in {1..350}; echo $nt $n; ./test $nt $n 2>> speedups.txt; done; done

Speedup by vectorization

Intel Xeon Phi has a 512 bit of space for simultaneous computation, which means it can calculate 8 double (or 16 single) operations at the same time. This is called vectorization and greatly improves code execution.

Consider the following code of speedtest.cpp:

 1 #include <cmath>
 2 #include <iostream>
 3 
 4 int main() {
 5     const int N = 104;
 6     double a[N];
 7     for (int i = 0; i < 1e5; i++)
 8         for (int j = 0; j < N; j++)
 9             a[j] = std::sin(std::exp(a[j]-j)*3 * i + i*j);
10     std::cout << a[4] << "\n";
11     return 0;
12 }

Intel's C++ compiler ICPC will successfully vectorize the inner for loop, so that it will run significantly faster than with vectorization disabled.

The code can be compiled with or without vectorization

$ icpc speedtest.cpp -o vectorized_speedtest -O3
$ icpc speedtest.cpp -o unvectorized_speedtest -O3 -no-vec

The below table shows execution times of the code displayed before on different machines with different settings. Two times represent execution time with double and float data type, respectively.

Machine	ASUS ZenBook Pro UX501VW	Intel® Xeon® CPU E5-2620 v3	Intel® Xeon® CPU E5-2620 v3	Intel® Xeon® CPU E5-2620 v3	Intel® Xeon Phi™ Coprocessor SE10/7120	Intel® Xeon Phi™ Coprocessor SE10/7120
Compiler	g++-6.3.1	g++-4.8.5	icpc-16.0.1	icpc-16.0.1 -no-vec	icpc-16.0.1 -mmic	icpc-16.0.1 -mmic -no-vec
Double time[s]	0.63 - 0.66	0.65 - 0.66	0.155 - 0.160	0.50 - 0.51	0.25 - 0.26	11.1 - 11.2
Float time[s]	0.65 - 0.71	0.53 - 0.55	0.155 - 0.160	0.17 - 0.19	0.37 - 0.38	4.2 - 4.3

We can see massive 44 fold speedup with and without vectorization.

Code incapable of vectorization

On the other hand there is a very similar code that can not be vectorized. Now all iterations of the inner loop access the same variable instead of each its own element in a list. ICPC is now unable to vectorize the code resulting in no difference when using -no-vec compile flag.

 1 #include <cmath>
 2 #include <iostream>
 3 
 4 int main() {
 5     const int N = 104;
 6     double a;
 7     for (int i = 0; i < 1e5; i++)
 8         for (int j = 0; j < N; j++)
 9             a = std::sin(std::exp(a-j)*3 * i + i*j);
10     std::cout << a << "\n";
11     return 0;
12 }

Machine	ASUS ZenBook Pro UX501VW	Intel® Xeon® CPU E5-2620 v3	Intel® Xeon® CPU E5-2620 v3	Intel® Xeon® CPU E5-2620 v3	Intel® Xeon Phi™ Coprocessor SE10/7120	Intel® Xeon Phi™ Coprocessor SE10/7120
Compiler	g++-6.3.1	g++-4.8.5	icpc-16.0.1	icpc-16.0.1 -no-vec	icpc-16.0.1 -mmic	icpc-16.0.1 -mmic -no-vec
Double time[s]	0.80 - 0.82	0.72 - 0.73	0.58 - 0.59	0.58 - 0.59	10.9 - 11.0	10.9 - 11.0
Float time[s]	0.69 - 0.72	0.66 - 0.67	0.32 - 0.33	0.32 - 0.34	4.1 - 4.2	4.1 - 4.2

Speedup by vectorization and parallelization

Consider the following code:

 1 #include <stdio.h>
 2 int main(){
 3     double *a, *b, *c;
 4     int i,j,k, ok, n=1000;  // or n=10000
 5     // allocated memory on the heap aligned to 64 byte boundary
 6     ok = posix_memalign((void**)&a, 64, n*n*sizeof(double));
 7     ok = posix_memalign((void**)&b, 64, n*n*sizeof(double));
 8     ok = posix_memalign((void**)&c, 64, n*n*sizeof(double));
 9     // initialize matrices
10     for (i = 0; i < n*n; ++i) {
11         a[i] = 1;
12         b[i] = 1;
13         c[i] = 1;
14     }
15     //parallelize via OpenMP on MIC
16     #pragma omp parallel for
17     for( i = 0; i < n; i++ ) {
18         for( k = 0; k < n; k++ ) {
19             #pragma vector aligned
20             #pragma ivdep
21             for( j = 0; j < n; j++ ) {
22                 //c[i][j] = c[i][j] + a[i][k]*b[k][j];
23                 c[i*n+j] = c[i*n+j] + a[i*n+k]*b[k*n+j];
24             }
25         }
26     }
27     printf("%f\n", c[n]);
28 }

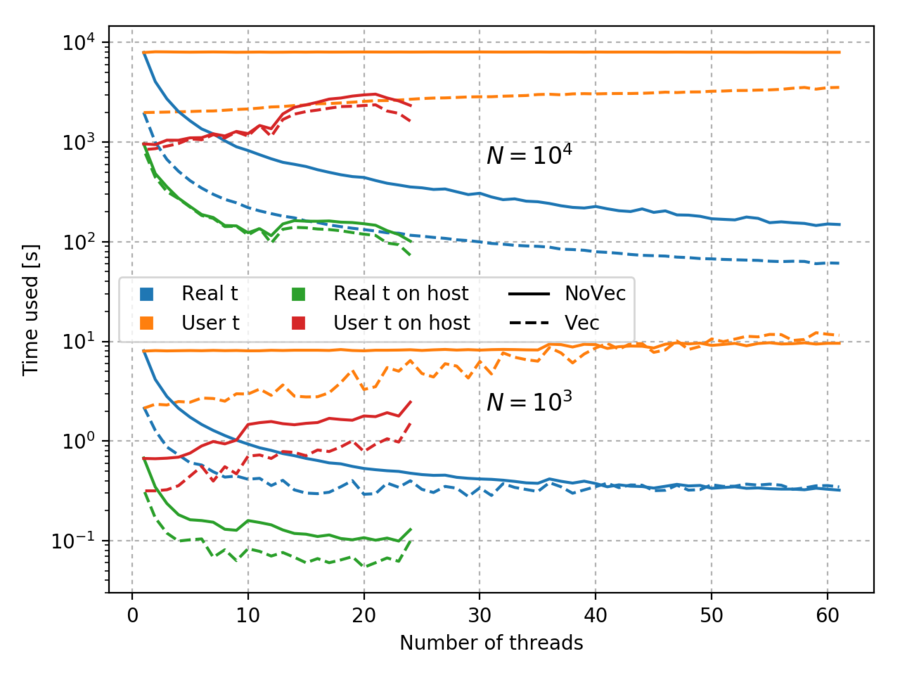
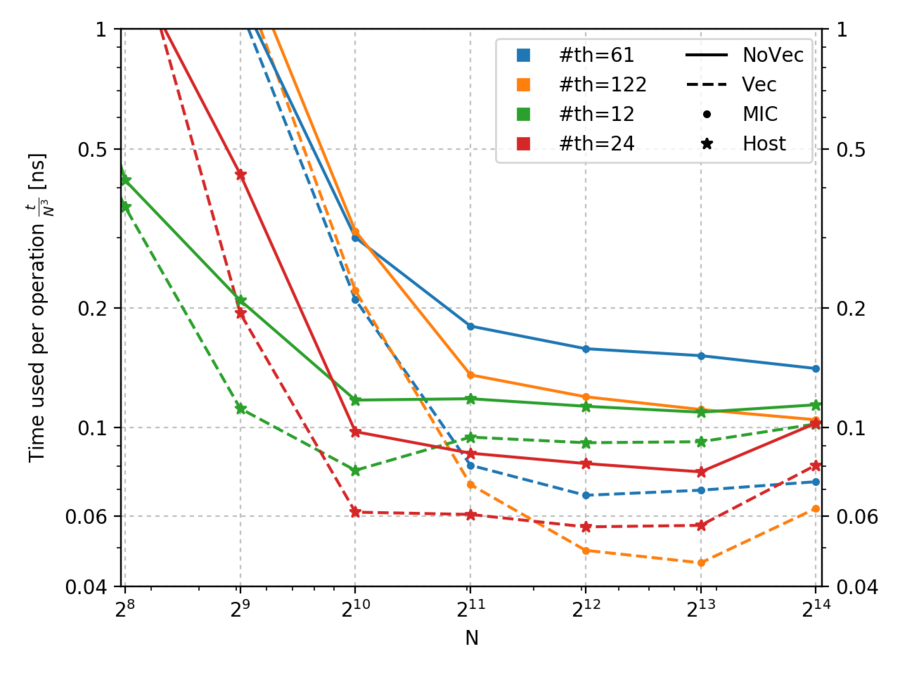
It is designed to be parallelizable and vectorizable. But with smaller systems (N=1000) we lose the benefits of vectorization with larger number of threads used.

However even the larger test case (N=10000) is barely faster than execution on the host processor. With 61 threads and vectorization it runs for a flat minute, where the host with 24 threads needs 1 minute and 15 seconds.

It is interesting to note that so-called "real time", i.e. the total processor time used, behaves differently for vectorized and nonvectorized code. For $N=10^4$ nonvectorized code constantly uses 133 minutes for completion regardless of thread number, but vectorized code goes from 33 minutes with one thread to an hour of total processing time with 61 threads. Similarly with $N=10^3$ and 61 threads nonvectorized code uses 125% of it beginning processing time, where for vectorized that figure is 600%.

Figure 3: Times used for the sample problem with and without vectorization using different number threads for two different N.

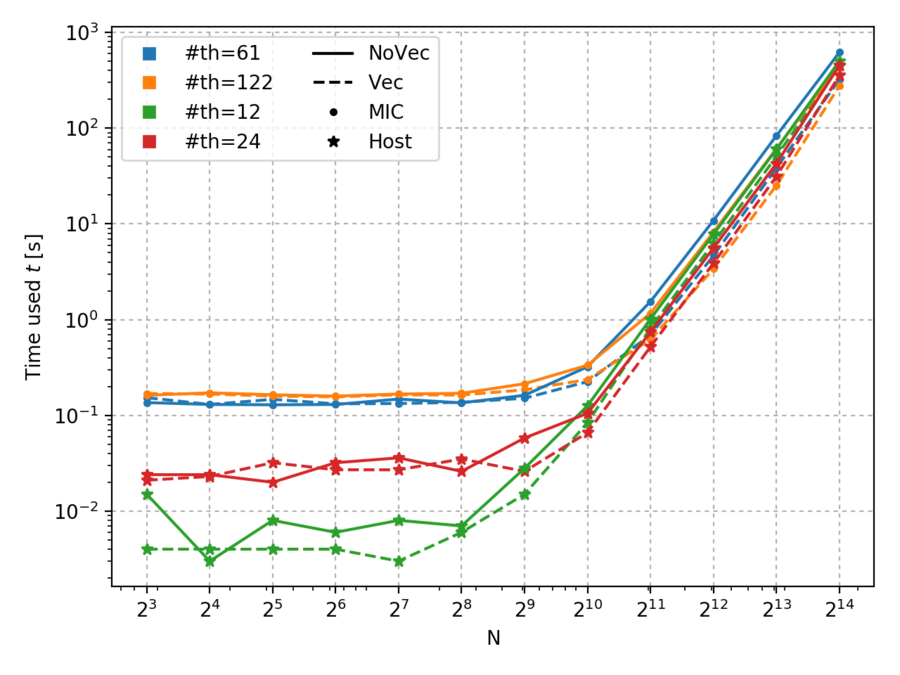
Below is a scan over different sizes $N$. Two parallelization regimes were used; Number of threads equal to the physical number of cores, and twice as many threads to take advantage of hyperthreading. All modes of execution show the same basic shape. All are inefficient for small $N$ but approach the complexity $N^3$ for large $N$.

Figure 4: Times used for a single operation with and without vectorization for different N.

Below we take a closer look at the time used for a single operation for larger $N$.

Figure 5: Times used for the sample problem with and without vectorization for different N.